
【题目】如图,三棱柱![]() 中,
中, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() 是
是![]() 上的动点,
上的动点, ![]() .
.
(Ⅰ)若点![]() 是
是![]() 中点,证明:平面
中点,证明:平面![]() 平面
平面![]() ;
;
(Ⅱ)判断点![]() 到平面
到平面![]() 的距离是否为定值?若是,求出定值;若不是,请说明理由.
的距离是否为定值?若是,求出定值;若不是,请说明理由.

科目:高中数学 来源: 题型:
【题目】园林管理处拟在公园某区域规划建设一半径为![]() 米圆心角为
米圆心角为![]() (弧度)的扇形景观水池,其中
(弧度)的扇形景观水池,其中![]() 为扇形
为扇形![]() 的圆心,同时紧贴水池周边建一圈理想的无宽度步道,要求总预算费用不超过
的圆心,同时紧贴水池周边建一圈理想的无宽度步道,要求总预算费用不超过![]() 万元,水池造价为每平方米
万元,水池造价为每平方米![]() 元,步道造价为每米
元,步道造价为每米![]() 元.
元.
(1)当![]() 和
和![]() 分别为多少时,可使广场面积最大,并求出最大值;
分别为多少时,可使广场面积最大,并求出最大值;
(2)若要求步道长为![]() 米,则可设计出水池最大面积是多少.
米,则可设计出水池最大面积是多少.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,已知下列条件解三角形:
①A=60°,a= ![]() ,b=1;
,b=1;
②A=30°,a=1,b=2;
③A=30°,c=10,a=6;
④A=30°,c=10,a=5,
其中有唯一解的序号为( )
A.①②③
B.①②④
C.②③④
D.①③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设点P的坐标为(x﹣3,y﹣2).
(1)在一个盒子中,放有标号为1,2,3的三张卡片,现在从盒子中随机取出一张卡片,记下标号后把卡片放回盒中,再从盒子中随机取出一张卡片记下标号,记先后两次抽取卡片的标号分别为x、y,求点P在第二象限的概率;
(2)若利用计算机随机在区间[0,3]上先后取两个数分别记为x、y,求点P在第三象限的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(12分)为了监控某种零件的一条生产线的生产过程,检验员每天从该生产线上随机抽取16个零件,并测量其尺寸(单位:cm).根据长期生产经验,可以认为这条生产线正常状态下生产的零件的尺寸服从正态分布N(μ,σ2).
(1)假设生产状态正常,记X表示一天内抽取的16个零件中其尺寸在(μ–3σ,μ+3σ)之外的零件数,求P(X≥1)及X的数学期望;
(2)一天内抽检零件中,如果出现了尺寸在(μ–3σ,μ+3σ)之外的零件,就认为这条生产线在这一天的生产过程可能出现了异常情况,需对当天的生产过程进行检查.
(ⅰ)试说明上述监控生产过程方法的合理性;
(ⅱ)下面是检验员在一天内抽取的16个零件的尺寸:
9.95 | 10.12 | 9.96 | 9.96 | 10.01 | 9.92 | 9.98 | 10.04 |
10.26 | 9.91 | 10.13 | 10.02 | 9.22 | 10.04 | 10.05 | 9.95 |
经计算得![]() ,
,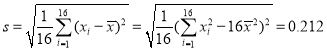 ,其中xi为抽取的第i个零件的尺寸,i=1,2,…,16.
,其中xi为抽取的第i个零件的尺寸,i=1,2,…,16.
用样本平均数![]() 作为μ的估计值
作为μ的估计值![]() ,用样本标准差s作为σ的估计值
,用样本标准差s作为σ的估计值![]() ,利用估计值判断是否需对当天的生产过程进行检查?剔除
,利用估计值判断是否需对当天的生产过程进行检查?剔除![]() 之外的数据,用剩下的数据估计μ和σ(精确到0.01).
之外的数据,用剩下的数据估计μ和σ(精确到0.01).
附:若随机变量Z服从正态分布N(μ,σ2),则P(μ–3σ<Z<μ+3σ)=0.997 4,0.997 416≈0.959 2,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com