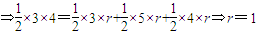Question

考虑坐标平面上以O（0，0），A（3，0），B（0，4）为顶点的三角形，令C₁，C₂分别为△OAB的外接圆、内切圆．请问下列哪些选项是正确的？
（1）C₁的半径为2
（2）C₁的圆心在直线y=x上
（3）C₁的圆心在直线4x+3y=12上
（4）C₂的圆心在直线y=x上
（5）C₂的圆心在直线4x+3y=6上．

Answer 1

【答案】分析：根据题意画出图形，如图所示，根据直角三角形的外接圆的圆心为斜边的中点，即斜边为外接圆的直径，利用两点间的距离公式求出|AB|，除以2即可得到C₁的半径，判断出选项（1）是错误的；
根据中点坐标公式求出线段AB的中点坐标即为外接圆的圆心坐标，即为C₁的圆心，代入y=x与4x+3y=12即可判断C₁的圆心在直线4x+3y=12上，不在y=x上，即选项（2）错误，选项（3）正确；
如图点P为三角形内切圆的圆心，作出点P到三角形三边的距离都为内切圆的半径r，把三角形AOB的面积分为三个三角形，根据三角形的面积公式即可列出关于r的方程，求出方程的解即可得到r的值，进而得到点P的坐标，判断出点P不在直线4x+3y=6上，在直线y=x上，即可得到选项（4）正确，（5）错误．
解答：解：O，A，B三点的位置如右图所示，C₁，C₂为△OAB的外接圆与内切圆，
∵△OAB为直角三角形，
∴C₁为以线段AB为直径的圆，故半径为，
所以（1）选项错误；
又C₁的圆心为线段AB的中点，此点在直线4x+3y=12上，
所以选项（2）错误，选项（3）正确；
如图，P为△OAB的内切圆C₂的圆心，
故P到△OAB的三边距离相等均为圆C₂的半径r．
连接PA，PB，PC，可得：S_△OAB=S_△POA+S_△PAB+S_△POB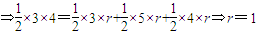

故P的坐标为（1，1），此点在y=x上．
所以选项（4）正确，选项（5）错误，
综上，正确的选项有（3）、（4）．
点评：此题考查学生掌握直角三角形的外接圆与内切圆的性质，灵活运用中点坐标公式及及两点间的距离公式化简求值，考查了数形结合的数学思想，是一道中档题．