
【题目】美国对中国芯片的技术封锁,这却激发了中国“芯”的研究热潮.某公司研发的![]() ,
,![]() 两种芯片都已经获得成功.该公司研发芯片已经耗费资金
两种芯片都已经获得成功.该公司研发芯片已经耗费资金![]() 千万元,现在准备投入资金进行生产.经市场调查与预测,生产
千万元,现在准备投入资金进行生产.经市场调查与预测,生产![]() 芯片的毛收入与投入的资金成正比,已知每投入
芯片的毛收入与投入的资金成正比,已知每投入![]() 千万元,公司获得毛收入
千万元,公司获得毛收入![]() 千万元;生产
千万元;生产![]() 芯片的毛收入
芯片的毛收入![]() (千万元)与投入的资金
(千万元)与投入的资金![]() (千万元)的函数关系为
(千万元)的函数关系为![]() ,其图像如图所示.
,其图像如图所示.

(1)试分别求出生产![]() ,
,![]() 两种芯片的毛收入
两种芯片的毛收入![]() (千万元)与投入资金
(千万元)与投入资金![]() (千万元)的函数关系式;
(千万元)的函数关系式;
(2)如果公司只生产一种芯片,生产哪种芯片毛收入更大?
(3)现在公司准备投入![]() 亿元资金同时生产
亿元资金同时生产![]() ,
,![]() 两种芯片,设投入
两种芯片,设投入![]() 千万元生产
千万元生产![]() 芯片,用
芯片,用![]() 表示公司所过利润,当
表示公司所过利润,当![]() 为多少时,可以获得最大利润?并求最大利润.(利润
为多少时,可以获得最大利润?并求最大利润.(利润![]() 芯片毛收入
芯片毛收入![]() 芯片毛收入
芯片毛收入![]() 研发耗费资金)
研发耗费资金)
【答案】(1)![]() ;(2)详见解析;(3)
;(2)详见解析;(3)![]() 千万元时,公司所获利润最大.最大利润
千万元时,公司所获利润最大.最大利润![]() 千万元.
千万元.
【解析】
(1)将![]()
![]() 代入
代入![]() ,求得
,求得![]() 的值,即可得到函数的解析式;
的值,即可得到函数的解析式;
(2)由题意,根据![]() 和
和![]() 的大小关系,可进行判定,得到答案.
的大小关系,可进行判定,得到答案.
(3)设投入![]() 千万元生产
千万元生产![]() 芯片,则投入
芯片,则投入![]() 千万元资金生产
千万元资金生产![]() 芯片,列出公司获利的函数关系式,利用二次函数的性质,即可求解.
芯片,列出公司获利的函数关系式,利用二次函数的性质,即可求解.
(1)设投入资金![]() 千万元,则生产
千万元,则生产![]() 芯片的毛收入
芯片的毛收入![]() ;
;
将![]()
![]() 代入
代入![]() ,得
,得![]()
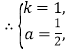
所以,生产![]() 芯片的毛收入
芯片的毛收入![]() .
.
(2)由![]() ,得
,得![]() ;由
;由![]() ,得
,得![]() ;
;
由![]() ,得
,得![]() .
.
所以,当投入资金大于千![]() 万元时,生产
万元时,生产![]() 芯片的毛收入大;
芯片的毛收入大;
当投入资金等于![]() 千万元时,生产
千万元时,生产![]() 、
、![]() 芯片的毛收入相等;
芯片的毛收入相等;
当投入资金小于![]() 千万元,生产
千万元,生产![]() 芯片的毛收入大.
芯片的毛收入大.
(3)公司投入![]() 亿元资金同时生产
亿元资金同时生产![]() ,
,![]() 两种芯片,设投入
两种芯片,设投入![]() 千万元生产
千万元生产![]() 芯片,则投入
芯片,则投入![]() 千万元资金生产
千万元资金生产![]() 芯片.公司所获利润
芯片.公司所获利润![]()
![]()
故当![]() ,即
,即![]() 千万元时,公司所获利润最大.最大利润
千万元时,公司所获利润最大.最大利润![]() 千万元.
千万元.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】AC为对称轴的抛物线的一部分,点B到边AC的距离为2km,另外两边AC,BC的长度分别为8km,2 ![]() km.现欲在此地块内建一形状为直角梯形DECF的科技园区.
km.现欲在此地块内建一形状为直角梯形DECF的科技园区. 
(1)求此曲边三角形地块的面积;
(2)求科技园区面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】医药公司针对某种疾病开发了一种新型药物,患者单次服用制定规格的该药物后,其体内的药物浓度![]() 随时间
随时间![]() 的变化情况(如图所示):当
的变化情况(如图所示):当![]() 时,
时,![]() 与
与![]() 的函数关系式为
的函数关系式为![]() (
(![]() 为常数);当
为常数);当![]() 时,
时,![]() 与
与![]() 的函数关系式为
的函数关系式为![]() (
(![]() 为常数).服药
为常数).服药![]() 后,患者体内的药物浓度为
后,患者体内的药物浓度为![]() ,这种药物在患者体内的药物浓度不低于最低有效浓度,才有疗效;而超过最低中毒浓度,患者就会有危险.
,这种药物在患者体内的药物浓度不低于最低有效浓度,才有疗效;而超过最低中毒浓度,患者就会有危险.
(1)首次服药后,药物有疗效的时间是多长?
(2)首次服药1小时后,可否立即再次服用同种规格的这种药物?
(参考数据:![]() ,
,![]() )
)

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() ,已知曲线
,已知曲线![]() 在点
在点![]() 处的切线与直线
处的切线与直线![]() 平行
平行
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)是否存在自然数![]() ,使得方程
,使得方程![]() 在
在![]() 内存在唯一的根?如果存在,求出
内存在唯一的根?如果存在,求出![]() ;如果不存在,请说明理由。
;如果不存在,请说明理由。
(Ⅲ)设函数![]() (
(![]() 表示
表示![]() 中的较小者),求
中的较小者),求![]() 的最大值。
的最大值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《城市规划管理意见》里面提出“新建住宅要推广街区制,原则上不再建设封闭住宅小区,已建成的封闭小区和单位大院要逐步打开”,这个消息在网上一石激起千层浪,各种说法不一而足.某网站为了解居民对“开放小区”认同与否,从![]() 岁的人群中随机抽取了
岁的人群中随机抽取了![]() 人进行问卷调查,并且做出了各个年龄段的频率分布直方图(部分)如图所示,同时对
人进行问卷调查,并且做出了各个年龄段的频率分布直方图(部分)如图所示,同时对![]() 人对这“开放小区”认同情况进行统计得到下表:
人对这“开放小区”认同情况进行统计得到下表:
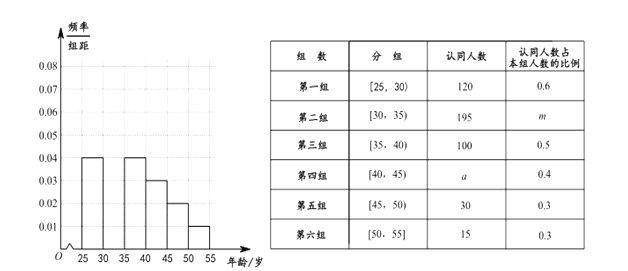
(Ⅰ)完成所给的频率分布直方图,并求![]() 的值;
的值;
(Ⅱ)如果从![]() 两个年龄段中的“认同”人群中,按分层抽样的方法抽取6人参与座谈会,然后从这6人中随机抽取2人作进一步调查,求这2人的年龄都在
两个年龄段中的“认同”人群中,按分层抽样的方法抽取6人参与座谈会,然后从这6人中随机抽取2人作进一步调查,求这2人的年龄都在![]() 内的概率 .
内的概率 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】邗江中学高二年级某班某小组共10人,利用寒假参加义工活动,已知参加义工活动次数为1,2,3的人数分别为3,3,4.现从这10人中选出2人作为该组代表参加座谈会.
(1)记“选出2人参加义工活动的次数之和为4”为事件![]() ,求事件
,求事件![]() 发生的概率;
发生的概率;
(2)设![]() 为选出2人参加义工活动次数之差的绝对值,求随机变量
为选出2人参加义工活动次数之差的绝对值,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义区间[x1 , x2]长度为x2﹣x1(x2>x1),已知函数f(x)= ![]() (a∈R,a≠0)的定义域与值域都是[m,n],则区间[m,n]取最大长度时a的值是 .
(a∈R,a≠0)的定义域与值域都是[m,n],则区间[m,n]取最大长度时a的值是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】心理学家发现视觉和空间能力与性别有关,某高中数学兴趣小组为了验证这个结论,从兴趣小组中抽取50名同学(男30女20),给所有同学几何题和代数题各一题,让各位同学自由选择一道题进行解答.选题情况如下表:(单位:人)
几何题 | 代数题 | 合计 | ||
男同学 | 22 | 8 | 30 | |
女同学 | 8 | 12 | 20 | |
合计 | 30 | 20 | 50 |
(1)能否据此判断有![]() 的把握认为视觉和空间能力与性别有关?
的把握认为视觉和空间能力与性别有关?
(2)以上列联表中女生选做几何题的频率作为概率,从该校1500名女生中随机选6名女生,记6名女生选做几何题的人数为![]() ,求
,求![]() 的数学期望
的数学期望![]() 和方差
和方差![]() .
.
附表:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
参考公式:![]() ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() (
(![]() ).
).
(1)当![]() 时,求关于
时,求关于![]() 的不等式
的不等式![]() 的解集;
的解集;
(2)若f(x)是偶函数,求k的值;
(3)在(2)条件下,设![]() ,若函数
,若函数![]() 与
与![]() 的图象有公共点,求实数b的取值范围.
的图象有公共点,求实数b的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com