
【题目】现有一长为100码,宽为80码,球门宽为8码的矩形足球运动场地,如图所示,其中![]() 是足球场地边线所在的直线,球门
是足球场地边线所在的直线,球门![]() 处于所在直线的正中间位置,足球运动员(将其看做点
处于所在直线的正中间位置,足球运动员(将其看做点![]() )在运动场上观察球门的角
)在运动场上观察球门的角![]() 称为视角.
称为视角.
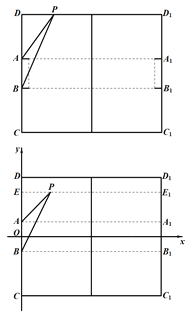
(1)当运动员带球沿着边线![]() 奔跑时,设
奔跑时,设![]() 到底线的距离为
到底线的距离为![]() 码,试求当
码,试求当![]() 为何值时
为何值时![]() 最大;
最大;
(2)理论研究和实践经验表明:张角![]() 越大,射门命中率就越大.现假定运动员在球场都是沿着垂直于底线的方向向底线运球,运动到视角最大的位置即为最佳射门点,以
越大,射门命中率就越大.现假定运动员在球场都是沿着垂直于底线的方向向底线运球,运动到视角最大的位置即为最佳射门点,以![]() 的中点为原点建立如图所示的直角坐标系,求在球场区域
的中点为原点建立如图所示的直角坐标系,求在球场区域![]() 内射门到球门
内射门到球门![]() 的最佳射门点的轨迹.
的最佳射门点的轨迹.
科目:高中数学 来源: 题型:
【题目】某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费对年销售量(单位:t)的影响.该公司对近5年的年宣传费和年销售量数据进行了研究,发现年宣传费x(万元)和年销售量y(单位:t)具有线性相关关系,并对数据作了初步处理,得到下面的一些统计量的值.

(1)根据表中数据建立年销售量y关于年宣传费x的回归方程;
(2)已知这种产品的年利润z与x,y的关系为![]() ,根据(1)中的结果回答下列问题:
,根据(1)中的结果回答下列问题:
①当年宣传费为10万元时,年销售量及年利润的预报值是多少?
②估算该公司应该投入多少宣传费,才能使得年利润与年宣传费的比值最大.
附:回归方程![]() 中的斜率和截距的最小二乘估计公式分别为
中的斜率和截距的最小二乘估计公式分别为

参考数据:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)![]() x2﹣xlnx,g(x)=(m﹣x)lnx+(1﹣m)x(m<0).
x2﹣xlnx,g(x)=(m﹣x)lnx+(1﹣m)x(m<0).
(1)讨论函数f′(x)的单调性;
(2)求函数F(x)=f(x)﹣g(x)在区间[1,+∞)上的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() ,点
,点![]() 为其右焦点,过点
为其右焦点,过点![]() 的直线与椭圆
的直线与椭圆![]() 相交于点
相交于点![]() ,
,![]() .
.
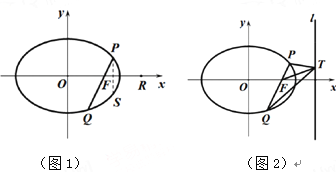
(1)当点![]() 在椭圆
在椭圆![]() 上运动时,求线段
上运动时,求线段![]() 的中点
的中点![]() 的轨迹方程;
的轨迹方程;
(2)如图1,点![]() 的坐标为
的坐标为![]() ,若点
,若点![]() 是点
是点![]() 关于
关于![]() 轴的对称点,求证:点
轴的对称点,求证:点![]() ,
,![]() ,
,![]() 共线;
共线;
(3)如图2,点![]() 是直线
是直线![]() 上的任意一点,设直线
上的任意一点,设直线![]() ,
,![]() ,
,![]() 的斜率分别为
的斜率分别为![]() ,
,![]() ,
,![]() ,求证
,求证![]() ,
,![]() ,
,![]() 成等差数列.
成等差数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】高三年级有500名学生,为了了解数学科的学习情况,现从中随机抽出若干名学生在一次测试中的数学成绩,制成如下频率分布表:
分组 | 频数 | 频率 |
|
|
|
|
| |
|
| |
| 12 |
|
|
| |
| 4 |
|
|
| |
合计 |
|
![]() 根据上面图表,求
根据上面图表,求![]() 处的数值
处的数值
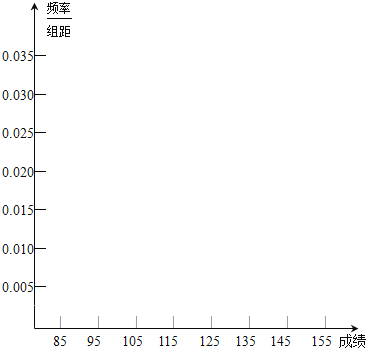
![]() 在所给的坐标系中画出
在所给的坐标系中画出![]() 的频率分布直方图;
的频率分布直方图;
![]() 根据题中信息估计总体平均数,并估计总体落在
根据题中信息估计总体平均数,并估计总体落在![]() 中的概率.
中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在棱长为1的正方体![]() 中,点
中,点![]() 是对角线
是对角线![]() 上的动点(点
上的动点(点![]() 与
与![]() 不重合),则下列结论正确的是__________
不重合),则下列结论正确的是__________
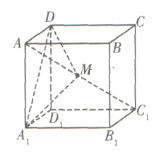
①存在点![]() ,使得平面
,使得平面![]() 平面
平面![]() ;
;
②存在点![]() ,使得平面
,使得平面![]() 平面
平面![]() ;
;
③![]() 的面积可能等于
的面积可能等于![]() ;
;
④若![]() 分别是
分别是![]() 在平面
在平面![]() 与平面
与平面![]() 的正投影的面积,则存在点
的正投影的面积,则存在点![]() ,使得
,使得![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 上的动点
上的动点![]() 到点
到点![]() 的距离减去
的距离减去![]() 到直线
到直线![]() 的距离等于1.
的距离等于1.
(1)求曲线![]() 的方程;
的方程;
(2)若直线 ![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点,求证:直线
两点,求证:直线![]() 与直线
与直线![]() 的倾斜角互补.
的倾斜角互补.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com