
【题目】在正方形![]() 中,
中, ![]() 的中点为点
的中点为点![]() ,
, ![]() 的中点为点
的中点为点![]() ,沿
,沿![]() 将
将![]() 向上折起得到
向上折起得到![]() ,使得面
,使得面![]() 面
面![]() ,此时点
,此时点![]() 位于点
位于点![]() 处.
处.
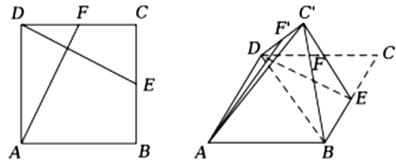
(Ⅰ)证明: ![]() ;
;
(Ⅱ)求面![]() 与面
与面![]() 所成二面角的正弦值.
所成二面角的正弦值.
【答案】(Ⅰ)(Ⅱ)![]()
【解析】试题分析:(Ⅰ)利用折叠前后的不变量得到有关垂直关系,进而利用线面垂直的判定定理得到线面垂直,再利用线面垂直的性质得到线线垂直;(Ⅱ)同(Ⅰ)证明有关线面垂直和线线垂直,进而建立适当的空间直角坐标系,利用空间向量进行求解.
试题解析:(Ⅰ)证明:连接![]() ,交
,交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() ,
, ![]() ,
,
如图所示,在正方形![]() 中,
中, ![]() 为
为![]() 中点,
中点, ![]() 为
为![]() 中点,所以
中点,所以![]() ;
;
由于![]() 为
为![]() 沿着
沿着![]() 翻折而来,从而
翻折而来,从而![]() ,所以
,所以![]() 面
面![]() ,
,
而![]() 在平面
在平面![]() 内,所以
内,所以![]() .
.

(Ⅱ)设![]() 中点为
中点为![]() ,连接
,连接![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() . 同(Ⅰ)可证
. 同(Ⅰ)可证![]() ,从而面
,从而面![]() 面
面![]() ,所以
,所以![]() ;由
;由![]() 面
面![]() ,可得面
,可得面![]() 面
面![]() ,又因为面
,又因为面![]() 面
面![]() ,且面
,且面![]() 与面
与面![]() 相交于
相交于![]() ,所以
,所以![]() 面
面![]() .
.
设![]() 为原点,过点
为原点,过点![]() 作
作![]() 轴平行于
轴平行于![]() ,作
,作![]() 轴平行于
轴平行于![]() ,
, ![]() 为
为![]() 轴,如图所示,不妨设正方形
轴,如图所示,不妨设正方形![]() 边长为3,从而
边长为3,从而![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
又因为![]() ,所以
,所以![]() ,
, ![]() ,在直角
,在直角![]() 中,由勾股定理可得
中,由勾股定理可得![]() ,
,
所以![]() ,即
,即![]() ,所以可以求得面
,所以可以求得面![]() 的法向量
的法向量![]() 为
为![]() ,面
,面![]() 的法向量
的法向量![]() 为
为![]() ,所以可以得出法向量
,所以可以得出法向量![]() ,则所求二面角的正弦值为
,则所求二面角的正弦值为![]() .
.



 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点为
的焦点为![]() ,抛物线上横坐标为
,抛物线上横坐标为![]() 的点到抛物线顶点的距离与该点到抛物线准线的距离相等。
的点到抛物线顶点的距离与该点到抛物线准线的距离相等。
(1)求抛物线![]() 的方程;
的方程;
(2)设直线![]() 与抛物线
与抛物线![]() 交于
交于![]() 两点,若
两点,若![]() ,求实数
,求实数![]() 的值。
的值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,边长为2的菱形ABCD中,∠A=60°,E、F分别是BC,DC的中点,G为 BF、DE的交点,若 ![]() =
= ![]()
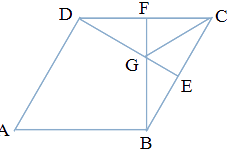
(1)试用 ![]() ,
, ![]() 表示
表示 ![]() ,
, ![]() ,
, ![]() ;
;
(2)求 ![]()
![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题错误的是( )
A. 如果平面![]() 平面
平面![]() ,那么平面
,那么平面![]() 内所有直线都垂直于平面
内所有直线都垂直于平面![]()
B. 如果平面![]() 平面
平面![]() ,那么平面
,那么平面![]() 内一定存在直线平行于平面
内一定存在直线平行于平面![]()
C. 如果平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
, ![]() ,那么
,那么![]() 平面
平面![]()
D. 如果平面![]() 不垂直于平面
不垂直于平面![]() ,那么平面
,那么平面![]() 内一定不存在直线垂直于平面
内一定不存在直线垂直于平面![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某书店销售刚刚上市的某知名品牌的高三数学单元卷,按事先拟定的价格进行5天试销,每种单价试销1天,得到如表数据:
单价x(元) | 18 | 19 | 20 | 21 | 22 |
销量y(册) | 61 | 56 | 50 | 48 | 45 |
(1)求试销5天的销量的方差和y对x的回归直线方程;
(2)预计今后的销售中,销量与单价服从(1)中的回归方程,已知每册单元卷的成本是14元,
为了获得最大利润,该单元卷的单价应定为多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在(0,2π)内,使sinx﹣cosx<0成立的x取值范围是( )
A.( ![]() ,
, ![]() )
)
B.(0, ![]() )
)
C.( ![]() ,π)∪(
,π)∪( ![]() ,2π)
,2π)
D.(0, ![]() )∪(
)∪( ![]() ,2π)
,2π)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π,x∈R)在一个周期内的图象如图所示,则函数的解析式为 . 直线y= ![]() 与函数y=f(x)(x∈R)图象的所有交点的坐标为 .
与函数y=f(x)(x∈R)图象的所有交点的坐标为 . 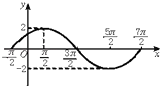
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数y=sin(2ωx+φ)(ω>0,0<φ<π)的最小正周期为π,且函数图象关于点(﹣ ![]() ,0)对称,则函数的解析式为( )
,0)对称,则函数的解析式为( )
A.y=sin(4x+ ![]() )
)
B.y=sin(2x+ ![]() )
)
C.y=sin(2x+ ![]() )
)
D.y=sin(4x+ ![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com