
【题目】已知函数f(x)=emx+x2﹣mx(m∈R).
(1)当m=1时,求函数f(x)的单调区间;
(2)若m<0,且曲线y=f(x)在点(1,f(1))处的切线与直线x+(e+1)y=0垂直.
(i)当x>0时,试比较f(x)与f(﹣x)的大小;
(ii)若对任意x1 , x2(x1≠x2),且f(x1)=f(x2),证明:x1+x2<0.
【答案】
(1)解:当m=1时,f′(x)=ex+2x﹣1=(ex﹣1)+2x,
若x>0,则ex﹣1>0,f′(x)>0,
若x<0,则ex﹣1<0,f′(x)<0,
综上,f(x)在(0,+∞)递增,在(﹣∞,0)递减;
(2)解:∵曲线y=f(x)在点(1,f(1))处的切线与直线x+(e+1)y=0垂直,
且f′(x)=m(emx﹣1)+2x,∴f′(1)=mem+2﹣m=e+1,
故mem﹣m=e﹣1,令h(m)=mem﹣m﹣e﹣1,
则h′(m)=em+mem﹣1,∵m>0,∴h′(m)>0,
∵h(1)=0,∴m>0,方程mem﹣m=e﹣1有唯一解m=1,
(i)当x>0时,
令g(x)=f(x)﹣f(﹣x)=ex﹣e﹣x﹣2x,
则g′(x)=ex+e﹣x﹣2>2﹣2=0,
∴g(x)在x>0时递增,即g(x)>g(0)=0,
故x>0时,f(x)>f(﹣x),
(ii)若对任意x1,x2(x1≠x2),且f(x1)=f(x2),
由(1)得:x1,x2必一正一负,
不妨设x1<0<x2,由(i)得:f(x1)﹣f(x2)>f(﹣x2),
而由(1)得:m=1时,函数f(x)在(﹣∞,0)递减,
∴x1<﹣x2,即x1+x2<0.
【解析】(1)将m=1代入f(x),求出f(x)的导数,从而求出函数的单调区间;(2)求出f(x)的导数,得到mem﹣m=e﹣1,令h(m)=mem﹣m﹣e﹣1,求出h(m)的导数,得到m的值;(i)根据做差法判断即可;(ii)问题转化为f(x1)﹣f(x2)>f(﹣x2),根据函数的单调性判断即可.
【考点精析】通过灵活运用利用导数研究函数的单调性,掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减即可以解答此题.
在这个区间单调递减即可以解答此题.


科目:高中数学 来源: 题型:
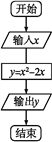
【题目】求函数y=![]() 的值的程序框图如图所示.
的值的程序框图如图所示.
(1)指出程序框图中的错误,并写出算法;
(2)重新绘制解决该问题的程序框图,并回答下面提出的问题.
①要使输出的值为正数,输入的x的值应满足什么条件?
②要使输出的值为8,输入的x值应是多少?
③要使输出的y值最小,输入的x值应是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,四棱锥![]() ,侧面
,侧面![]() 是边长为2的正三角形,且平面
是边长为2的正三角形,且平面![]() 平面
平面![]() ,底面
,底面![]() 是菱形,且
是菱形,且![]() ,
, ![]() 为棱
为棱![]() 上的动点,且
上的动点,且![]() .
.

(1)求证: ![]() ;
;
(2)试确定![]() 的值,使得二面角
的值,使得二面角![]() 的余弦值为
的余弦值为![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四棱柱ABCD﹣A1B1C1D1的侧棱AA1⊥底面ABCD,ABCD是等腰梯形,AB∥DC,AB=2,AD=1,∠ABC=60°,E为A1C的中点 
(1)求证:D1E∥平面BB1C1C;
(2)求证:BC⊥A1C;
(3)若A1A=AB,求二面角A1﹣AC﹣B1的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,棱柱ABCD-A1B1C1D1中,底面ABCD是平行四边形,侧棱AA1⊥底面ABCD,AB=1,AC=![]() ,BC=BB1=2.
,BC=BB1=2.

(Ⅰ)求证:AC⊥平面ABB1A1;
(Ⅱ)求点D到平面ABC1的距离d.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数y=f(x)满足f(﹣x)+f(x)=0且f(x+1)=f(x﹣1),若x∈(0,1)时,f(x)=log2 ![]() ,则y=f(x)在(1,2)内是( )
,则y=f(x)在(1,2)内是( )
A.单调增函数,且f(x)<0
B.单调减函数,且f(x)<0
C.单调增函数,且f(x)>0
D.单调增函数,且f(x)>0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC-A1B1C1中,CC1⊥底面ABC,AC⊥CB,点M和N分别是B1C1和BC的中点.

(1)求证:MB∥平面AC1N;
(2)求证:AC⊥MB.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com