练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    在△ABC中，角A，B，C所对的边长分别为a，b，c．若asinA+bsinB-csinC=
    		3
    asinB．则角C等于（　　）
    A、
    π
    6
    B、
    π
    4
    C、
    π
    3
    D、
    5π
    6
    考点：正弦定理
    专题：解三角形
    分析：根据正弦定理和余弦定理将条件进行化简即可得到结论．
    解答：解：∵asinA+bsinB-csinC=
    		3
    asinB．
    ∴由正弦定理可得a2+b2-c2=
    		3
    ab，
    ∴由余弦定理可得cosC=
    a2+b2-c2
    2ab
    =
    		3
    ab
    2ab
    =
    		3
    2
    ，
    ∵0＜C＜π，
    ∴C=
    π
    6
    ，
    故选：A．
    点评：本题主要考查三角函数角的求解，利用正弦定理和余弦定理是解决本题的关键．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知直线a，b，c，d，“a∥b”的充分条件是（　　）
    A、a⊥c，b⊥c
    B、a∩b=∅
    C、a∥c，b∥c
    D、a∥c，b⊥c

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设f（x）是定义在[-2，2]上的奇函数，若f（x）在[-2，0]上单调递减，则使f（a2-a）＜0成立的实数a的取值范围是（　　）
    A、[-1，2]
    B、[-1，0）∪（1，2]
    C、（0，1）
    D、（-∞，0）∪（1，+∞）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设全集U={1，2，3，4，5}，集合A={1，3，5}，集合B={3，4}，则（∁UA）∩B=（　　）
    A、{3}B、{4}
    C、{3，4}D、{2，3，4}

    查看答案和解析>>

    科目：高中数学 来源： 题型：

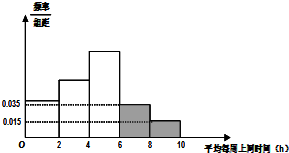    为了解高中生平均每周上网玩微信，刷微博，打游戏享受智能手机带来的娱乐生活体验，从高三年级学生中抽取部分同学进行调查，将所得的数据整理如下，画出频率分布直方图（如图），其中频率分布直方图从左至右前3个小组的频率之比为1：3：5，第二组的频数为150，则被调查的人数应为（　　）
    A、600B、400
    C、700D、500

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    下列说法中正确的是（　　）
    A、若分类变量X和Y的随机变量K2的观测值k越大，则“X与Y相关”的可信程度越小
    B、对于自变量x和因变量y，当x取值一定时，y的取值具有一定的随机性，x，y间的这种非确定关系叫做函数关系
    C、相关系数r2越接近1，表明两个随机变量线性相关性越弱
    D、若分类变量X与Y的随机变量K2的观测值k越小，则两个分类变量有关系的把握性越小

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知不等式|y+4|-|y|≤2x+
    a
    2x
    对任意实数x，y都成立，则常数a的最小值为（　　）
    A、1B、2C、3D、4

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数f（x）=x3+ax2+bx+c，其0＜f（-1）=f（-2）=f（-3）≤3，则（　　）
    A、c≤3B、3＜c≤6
    C、6＜c≤9D、c＞9

    查看答案和解析>>

    科目：高中数学 来源：2013-2014学年四川省高三三诊模拟理科数学试卷（解析版） 题型：选择题

    已知复数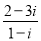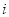（是虚数单位），它的实部与虚部的和是（ ）

    A.4 B.6 C.2 D.3

     

    查看答案和解析>>

    同步练习册答案