
【题目】已知极点与直角坐标系的原点重合,极轴与![]() 轴的正半轴重合,曲线
轴的正半轴重合,曲线![]() 的极坐标方程是
的极坐标方程是![]() ,直线
,直线![]() 的参数方程是
的参数方程是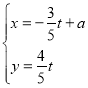 (
(![]() 为参数).
为参数).
(1)若![]() ,
,![]() 是圆
是圆![]() 上一动点,求点
上一动点,求点![]() 到直线
到直线![]() 的距离
的距离![]() 的最小值和最大值;
的最小值和最大值;
(2)直线![]() 与
与![]() 关于原点对称,且直线
关于原点对称,且直线![]() 截曲线
截曲线![]() 的弦长等于
的弦长等于![]() ,求
,求![]() 的值.
的值.
科目:高中数学 来源: 题型:
【题目】每年的3月12日是植树节,某公司为了动员职工积极参加植树造林,在植树节期间开展植树有奖活动,设有甲、乙两个摸奖箱,每位植树者植树每满30棵获得一次甲箱内摸奖机会,植树每满50棵获得一次乙箱内摸奖机会,每箱内各有10个球(这些球除颜色外全相同),甲箱内有红、黄、黑三种颜色的球,其中![]() 个红球,
个红球,![]() 个黄球,5个黑球,乙箱内有4个红球和6个黄球,每次摸一个球后放回原箱,摸得红球奖100元,黄球奖50元,摸得黑球则没有奖金.
个黄球,5个黑球,乙箱内有4个红球和6个黄球,每次摸一个球后放回原箱,摸得红球奖100元,黄球奖50元,摸得黑球则没有奖金.
(1)经统计,每人的植树棵数![]() 服从正态分布
服从正态分布![]() ,若其中有200位植树者参与了抽奖,请估计植树的棵数
,若其中有200位植树者参与了抽奖,请估计植树的棵数![]() 在区间
在区间![]() 内并中奖的人数(结果四舍五入取整数);
内并中奖的人数(结果四舍五入取整数);
附:若![]() ,则
,则![]() ,
,
![]() .
.
(2)若![]() ,某位植树者获得两次甲箱内摸奖机会,求中奖金额
,某位植树者获得两次甲箱内摸奖机会,求中奖金额![]() (单位:元)的分布列;
(单位:元)的分布列;
(3)某人植树100棵,有两种摸奖方法,
方法一:三次甲箱内摸奖机会;
方法二:两次乙箱内摸奖机会;
请问:这位植树者选哪一种方法所得奖金的期望值较大.
查看答案和解析>>
科目:高中数学 来源: 题型:
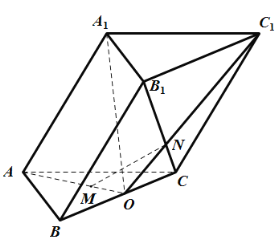
【题目】如图,斜三棱柱![]() 中,
中,![]() 是边长为2的正三角形,
是边长为2的正三角形,![]() 为
为![]() 的中点,
的中点,![]() 平面
平面![]() ,点
,点![]() 在
在![]() 上,
上,![]() ,
,![]() 为
为![]() 与
与![]() 的交点,且
的交点,且![]() 与平面
与平面![]() 所成的角为
所成的角为![]() .
.
(1)求证:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的正弦值.
的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
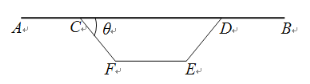
【题目】图1是某高架桥箱梁的横截面,它由上部路面和下部支撑箱两部分组成.如图2,路面宽度![]() ,下部支撑箱CDEF为等腰梯形(
,下部支撑箱CDEF为等腰梯形(![]() ),且
),且![]() .为了保证承重能力与稳定性,需下部支撑箱的面积为
.为了保证承重能力与稳定性,需下部支撑箱的面积为![]() ,高度为2m且
,高度为2m且![]() ,若路面AB.侧边CF和DE,底部EF的造价分别为4a千元/m,5a千元/m,6a千元/m(a为正常数),
,若路面AB.侧边CF和DE,底部EF的造价分别为4a千元/m,5a千元/m,6a千元/m(a为正常数),![]() .
.

(1)试用θ表示箱梁的总造价y(千元);
(2)试确定cosθ的值,使总造价最低?并求最低总造价.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在长方体![]() 中,
中,![]() 是
是![]() 的中点,点
的中点,点![]() 是
是![]() 上一点,
上一点,![]() ,
,![]() ,
,![]() .动点
.动点![]() 在上底面
在上底面![]() 上,且满足三棱锥
上,且满足三棱锥![]() 的体积等于1,则直线
的体积等于1,则直线![]() 与
与![]() 所成角的正切值的最大值为( )
所成角的正切值的最大值为( )

A.![]() B.
B.![]() C.
C.![]() D.2
D.2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】斜率为![]() 的直线
的直线![]() 过抛物线
过抛物线![]() :
:![]() 的焦点
的焦点![]() ,且与拋物线
,且与拋物线![]() 交于
交于![]() ,
,![]() 两点.
两点.
(1)设点![]() 在笫一象限,过
在笫一象限,过![]() 作拋物线
作拋物线![]() 的准线的垂线,
的准线的垂线,![]() 为垂足,且
为垂足,且![]() ,求点
,求点![]() 的坐标;
的坐标;
(2)过![]() 且与
且与![]() 垂直的直线
垂直的直线![]() 与圆
与圆![]() :
:![]() 交于
交于![]() ,
,![]() 两点,若
两点,若![]() 与
与![]() 面积之和为
面积之和为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校拟从甲、乙两名同学中选一人参加疫情知识问答竞赛,于是抽取了甲、乙两人最近同时参加校内竞赛的十次成绩,将统计情况绘制成如图所示的折线图.根据该折线图,下面结论正确的是( )
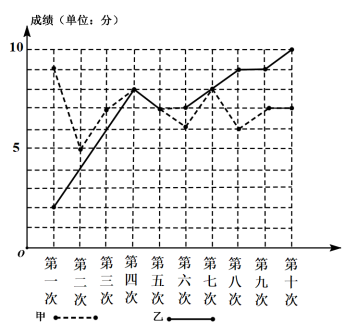
A.甲、乙成绩的中位数均为7
B.乙的成绩的平均分为6.8
C.甲从第四次到第六次成绩的下降速率要大于乙从第四次到第五次的下降速率
D.甲的成绩的方差小于乙的成绩的方差
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】农历五月初五是端午节,民间有吃粽子的习惯,粽子又称粽籺,俗称“粽子”,古称“角黍”,是端午节大家都会品尝的食品,传说这是为了纪念战国时期楚国大臣、爱国主义诗人屈原,如图所示,平行四边形形状的纸片是由六个边长为![]() 的正三角形构成的,将它沿虚线折起来,可以得到如图所示粽子形状的六面体,则该六面体的体积为______;若该六面体内有一球,则该球体积的最大值为______.
的正三角形构成的,将它沿虚线折起来,可以得到如图所示粽子形状的六面体,则该六面体的体积为______;若该六面体内有一球,则该球体积的最大值为______.
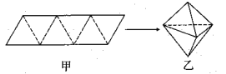
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com