
解析:若选择圆的一般形式:x2+y2+Dx+Ey+F=0,其中D、E、F为三个待定系数,则需依题意,建立起三个独立方程求解.
设圆的方程为x2+y2+Dx+Ey+F=0,其圆心为![]() .
.
∵圆过点A(2,-1),∴5+2D-E+F=0 ①
又圆心在直线2x+y=0上,
∴![]() ,即2D+E=0 ②
,即2D+E=0 ②
将y=x-1代入圆方程得
2x2+(D+E-2)x+(1-E+F)=0
Δ=(D+E-2)2-8(1-E+F)=0. ③
将①②代入③中,得(-D-2)2-8(1-2D-5)=0
即D2+20D+36=0,∴D=-2或D=-18.
代入①②,得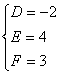 或
或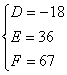
故所求圆的方程为x2+y2-2x+4y+3=0或x2+y2-18x+36y+67=0.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2010-2011学年广东省深圳市高三上学期第一次月考文科数学卷 题型:解答题
(本小题满分12分)
已知圆经过点A(2,-3)和B(-2,-5).
(1)若圆心在直线x-2y-3=0上,求圆的方程. (2)若圆的面积最小,求圆的方程;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com