
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是边长为
是边长为![]() 的菱形,
的菱形,![]() ,且平面
,且平面![]() 平面
平面![]() .
.
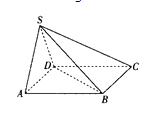
(1)证明:![]()
(2)求二面角![]() 的余弦值.
的余弦值.
 提分百分百检测卷系列答案
提分百分百检测卷系列答案科目:高中数学 来源: 题型:
【题目】在长方体![]() 中,
中,![]() ,过
,过![]() ,
,![]() ,
,![]() 三点的平面截去长方体的一个角后,得到如图所示的几何体
三点的平面截去长方体的一个角后,得到如图所示的几何体![]() ,这个几何体的体积为
,这个几何体的体积为![]() .
.

(1)求棱![]() 的长;
的长;
(2)求经过![]() ,
,![]() ,
,![]() ,
,![]() 四点的球的表面积和体积.
四点的球的表面积和体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】北京、张家口2022年冬奥会申办委员会在俄罗斯索契举办了发布会,某公司为了竞标配套活动的相关代言,决定对旗下的某商品进行一次评估,该商品原来每件售价为25元,年销售8万件.
(1)据市场调查,若价格每提高1元,销售量将相应减少2000件,要使销售的总收入不低于原收入,该商品每件定价最多为多少元?
(2)为了抓住申奥契机,扩大该商品的影响力,提高年销售量.公司决定立即对该商品进行全面技术革新和营销策略改革,并提高定价到![]() 元.公司拟投入
元.公司拟投入![]() 万作为技改费用,投入50万元作为固定宣传费用,投入
万作为技改费用,投入50万元作为固定宣传费用,投入![]() 万元作为浮动宣传费用.试问:当该商品改革后的销售量
万元作为浮动宣传费用.试问:当该商品改革后的销售量![]() 至少应达到多少万件时,才可能使改革后的销售收入不低于原收入与总投入之和?并求出此时商品的每件定价.
至少应达到多少万件时,才可能使改革后的销售收入不低于原收入与总投入之和?并求出此时商品的每件定价.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》是中国古代的数学专著,其中的“更相减损术”原文是:“可半者半之,不可半者,副置分母、子之数,以少减多,更相减损,求其等也以等数约之”即(如果需要对分数进行约分,那么)可以折半的话,就折半(也就是用2来约分).如果不可以折半的话,那么就比较分母和分子的大小,用大数减去小数,互相减来减去,一直到减数与差相等为止,用这个相等的数字来约分.如图是“更相减损术”的程序框图,如果输入![]() ,
,![]() ,则输出的
,则输出的![]() 值是( )
值是( )
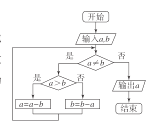
A.72B.70C.34D.36
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 在左、右焦点分别为
在左、右焦点分别为![]() ,
,![]() ,上顶点为点
,上顶点为点![]() ,若
,若![]() 是面积为
是面积为![]() 的等边三角形.
的等边三角形.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)已知![]() ,
,![]() 是椭圆
是椭圆![]() 上的两点,且
上的两点,且![]() ,求使
,求使![]() 的面积最大时直线
的面积最大时直线![]() 的方程(
的方程(![]() 为坐标原点).
为坐标原点).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,现有4种不同颜色给图中5个区域涂色,要求任意两个相邻区域不同色,共有______种不同涂色方法;若要求4种颜色都用上且任意两个相邻区域不同色,共有______种不同涂色方法.(用数字作答)
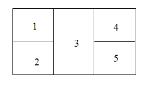
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在三棱柱![]() 中,底面
中,底面![]() 是以
是以![]() 为斜边的等腰直角三角形,侧面
为斜边的等腰直角三角形,侧面![]() 是菱形且与底面
是菱形且与底面![]() 垂直,
垂直,![]() ,点
,点![]() 是
是![]() 中点,点
中点,点![]() 是
是![]() 上靠近
上靠近![]() 点的三等分点.
点的三等分点.
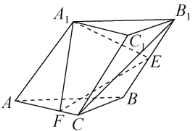
(1)证明:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com