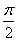练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    某学生对函数f(x)=2xcosx进行研究后，得出如下四个结论：
    （1）函数f(x)在[-π，0]上单调递增，在[0，π]上单调递减；
    （2）存在常数M＞0，使|f(x)|≤M|x|对一切实数x均成立；
    （3）点（，0）是函数y=f(x)图像的一个对称中心；
    （4）函数y=f(x)图像关于直线x=π对称；
    其中正确的是（    ）。（把你认为正确命题的序号都填上）
    ②
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：辽宁省沈阳二中2008－2009学年高三上学期期中考试(数学理) 题型：022

    某学生对函数f(x)＝xsinx进行研究后，得出如下结论：

    ①函数f(x)在上单调递增；

    ②存在常数M＞0，使f(x)≤M(x)对一切实数x均成立；

    ③函数f(x)在(0，π)上无最小值，但一定有最大值；

    ④点(π，0)是函数y＝f(x)图象的一个对称中心

    其中正确命题的序号是________．

    查看答案和解析>>

    科目：高中数学 来源：福建省四地六校2012届高三期中联考试题数学理科试题 题型：022

    某学生对函数f(x)＝2x·cosx的性质进行研究，得出如下的结论：

    ①函数f(x)在[－π，0]上单调递增，在[0，π]上单调递减；

    ②点(，0)是函数y＝f(x)图象的一个对称中心；

    ③函数y＝f(x)图象关于直线x＝π对称；

    ④存在常数M＞0，使|f(x)|≤M|x|对一切实数x均成立．

    其中正确的结论是________．(填写所有你认为正确结论的序号)

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    某学生对函数f(x)=xsinx进行研究后,得出如下四个结论:①函数f(x)在［-,］上单调递增;②存在常数M＞0,使|f(x)|≤M|x|对一切实数x均成立;③函数f(x)在(0,π)上无最小值,但一定有最大值;④点(π,0)是函数y=f(x)图象的一个对称中心.其中正确的是

    A.①③                B.②③                C.②④               D.①②④

    查看答案和解析>>

    科目：高中数学 来源：吉林省模拟题 题型：填空题

    某学生对函数f (x）=2xcosx进行研究后，得出如下四个结论：
    ①函数f(x)在[-π，0]上单调递增，在[0，π]上单调递减；
    ②存在常数M＞0，使|f(x)|≤M|x|对一切实数x均成立；
    ③点（，0）是函数f（x）图象的一个对称中心；
    ④函数y=f（x）图象关于直线x=π对称；
    其中正确的是（    ）。（把你认为正确命题的序号都填上）

    查看答案和解析>>

    同步练习册答案