
(14分)2006年5月3日进行抚仙湖水下考古,潜水员身背氧气瓶潜入湖底进行
考察,氧气瓶形状如图,其结构为一个圆柱和一个圆台的组合(设氧气瓶中氧气已充满,所
给尺寸是氧气瓶的内径尺寸),潜水员在潜入水下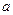 米的过程中,速度为
米的过程中,速度为 米/分,每分钟
米/分,每分钟
需氧量与速度平方成正比(当速度为1米/分时,每分钟需氧量为0.2L);在湖底工作时,
每分钟需氧量为0.4 L;返回水面时,速度也为 米/分,每分钟需氧量为0.2 L,若下
米/分,每分钟需氧量为0.2 L,若下
潜与上浮时速度不能超过p米/分,试问潜水员在湖底最多能工作多少时间?(氧气瓶体积
计算精确到1 L,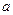 、p为常数,圆台的体积V=
、p为常数,圆台的体积V= ,其中h为高,r、R分
,其中h为高,r、R分
别为上、下底面半径.)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com