
【题目】已知圆![]() 与圆
与圆![]() 相外切,且与直线
相外切,且与直线![]() 相切.
相切.
(1)记圆心![]() 的轨迹为曲线
的轨迹为曲线![]() ,求
,求![]() 的方程;
的方程;
(2)过点![]() 的两条直线
的两条直线![]() 与曲线
与曲线![]() 分别相交于点
分别相交于点![]() 和
和![]() ,线段
,线段![]() 和
和![]() 的中点分别为
的中点分别为![]() .如果直线
.如果直线![]() 与
与![]() 的斜率之积等于1,求证:直线
的斜率之积等于1,求证:直线![]() 经过定点.
经过定点.
【答案】(1)![]() (2)见解析
(2)见解析
【解析】
(1)根据抛物线定义可知圆心![]() 的轨迹为抛物线,进而可得其轨迹方程.
的轨迹为抛物线,进而可得其轨迹方程.
(2)由题意可设直线![]() 的斜率为
的斜率为![]() ,则直线
,则直线![]() 的斜率为
的斜率为![]() ,表示出直线
,表示出直线![]() 的方程,联立直线与抛物线方程即可求得交点
的方程,联立直线与抛物线方程即可求得交点![]() 的坐标,进而以
的坐标,进而以![]() 代替点
代替点![]() 坐标中的
坐标中的![]() ,可得点
,可得点![]() 的坐标;即可表示出直线
的坐标;即可表示出直线![]() 的斜率及其方程,进而得所过定点的坐标.
的斜率及其方程,进而得所过定点的坐标.
(1)依题意![]() 等于
等于![]() 到直线
到直线![]() 的距离,
的距离,
故所求轨迹是以![]() 为焦点,以
为焦点,以![]() 为准线的抛物线.
为准线的抛物线.
故其轨迹![]() 的方程为
的方程为![]() .
.
(2)依题意直线![]() 斜率都存在且均不为
斜率都存在且均不为![]() ,
,
故设直线![]() 的斜率为
的斜率为![]() ,则直线
,则直线![]() 的斜率为
的斜率为![]() .
.
直线![]() 的方程为
的方程为![]() ,
,
即为![]() .
.
由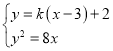 消去
消去![]() 整理得
整理得![]() ,
,
所以![]() ,点
,点![]() 的坐标为
的坐标为![]() ,
,
以![]() 代替点
代替点![]() 坐标中的
坐标中的![]() ,可得点
,可得点![]() 的坐标为
的坐标为![]() ,
,
所以直线![]() 的斜率
的斜率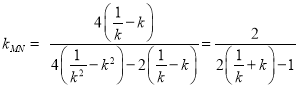 ,
,
所以直线![]() 的方程为
的方程为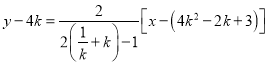 ,
,
即![]() .
.
故![]() 经过定点
经过定点![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】某便利店统计了今年第一季度各个品类的销售收入占比和净利润占比,并将部分品类的这两个数据制成如下统计图(注:销售收入占比![]() ,净利润占比
,净利润占比![]() ,净利润
,净利润![]() 销售收入
销售收入![]() 成本
成本![]() 各类费用),现给出下列判断:
各类费用),现给出下列判断:
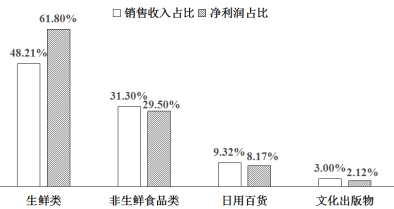
①该便利店第一季度至少有一种品类是亏损的;
②该便利店第一季度的销售收入中“生鲜类”贡献最大;
③该便利店第一季度“非生鲜食品类”的净利润一定高于“日用百货”的销售收入;
④该便利店第一季度“生鲜类”的销售收入比“非生鲜食品类”的销售收入多![]() .
.
则上述判断中正确的是( )
A.①②B.②③C.①④D.③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,随着全球石油资源紧张、大气污染日益严重和电池技术的提高,电动汽车已被世界公认为21世纪汽车工业改造和发展的主要方向.为了降低对大气的污染和能源的消耗,某品牌汽车制造商研发了两款电动汽车车型![]() 和车型
和车型![]() ,并在黄金周期间同时投放市场.为了了解这两款车型在黄金周的销售情况,制造商随机调查了5家汽车
,并在黄金周期间同时投放市场.为了了解这两款车型在黄金周的销售情况,制造商随机调查了5家汽车![]() 店的销量(单位:台),得到下表:
店的销量(单位:台),得到下表:
| 甲 | 乙 | 丙 | 丁 | 戊 |
车型 | 6 | 6 | 13 | 8 | 11 |
车型 | 12 | 9 | 13 | 6 | 4 |
(1)若从甲、乙两家![]() 店销售出的电动汽车中分别各自随机抽取1台电动汽车作满意度调查,求抽取的2台电动汽车中至少有1台是车型
店销售出的电动汽车中分别各自随机抽取1台电动汽车作满意度调查,求抽取的2台电动汽车中至少有1台是车型![]() 的概率;
的概率;
(2)现从这5家汽车![]() 店中任选3家举行促销活动,用
店中任选3家举行促销活动,用![]() 表示其中车型
表示其中车型![]() 销量超过车型
销量超过车型![]() 销量的
销量的![]() 店的个数,求随机变量
店的个数,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知点![]() 是
是![]() 轴下方(不含
轴下方(不含![]() 轴)一点,抛物线
轴)一点,抛物线![]() 上存在不同的两点
上存在不同的两点![]() 、
、![]() 满足
满足![]() ,
,![]() ,其中
,其中![]() 为常数,且
为常数,且![]() 、
、![]() 两点均在
两点均在![]() 上,弦
上,弦![]() 的中点为
的中点为![]() .
.
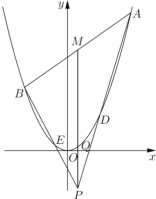
(1)若![]() 点坐标为
点坐标为![]() ,
,![]() 时,求弦
时,求弦![]() 所在的直线方程;
所在的直线方程;
(2)在(1)的条件下,如果过![]() 点的直线
点的直线![]() 与抛物线
与抛物线![]() 只有一个交点,过
只有一个交点,过![]() 点的直线
点的直线![]() 与抛物线
与抛物线![]() 也只有一个交点,求证:若
也只有一个交点,求证:若![]() 和
和![]() 的斜率都存在,则
的斜率都存在,则![]() 与
与![]() 的交点
的交点![]() 在直线
在直线![]() 上;
上;
(3)若直线![]() 交抛物线
交抛物线![]() 于点
于点![]() ,求证:线段
,求证:线段![]() 与
与![]() 的比为定值,并求出该定值.
的比为定值,并求出该定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆![]() 的焦距是
的焦距是![]() ,长轴长是短轴长3倍,任作斜率为
,长轴长是短轴长3倍,任作斜率为![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点(如图所示),且点
两点(如图所示),且点![]() 在直线
在直线![]() 的左上方.
的左上方.
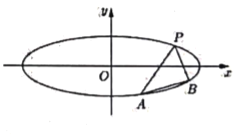
(1)求椭圆![]() 的方程;
的方程;
(2)若![]() ,求
,求![]() 的面积;
的面积;
(3)证明:![]() 的内切圆的圆心在一条定直线上。
的内切圆的圆心在一条定直线上。
查看答案和解析>>
科目:高中数学 来源: 题型:
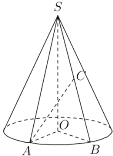
【题目】如图所示,圆锥的底面![]() 半径为2,
半径为2,![]() 是圆周上的定点,动点
是圆周上的定点,动点![]() 在圆周上逆时针旋转,设
在圆周上逆时针旋转,设![]() (
(![]() ),
),![]() 是母线
是母线![]() 的中点,已知当
的中点,已知当![]() 时,
时,![]() 与底面所成角为
与底面所成角为![]() .
.
(1)求该圆锥的侧面积;
(2)若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com