
【题目】已知函数![]()
(Ⅰ)设![]() ,若
,若![]() 的图象与x轴恰有两个不同的交点,求实数a的取值集合.
的图象与x轴恰有两个不同的交点,求实数a的取值集合.
(Ⅱ)求函数![]() 在区间
在区间![]() 上的最大值.
上的最大值.
【答案】(Ⅰ)![]() ;(Ⅱ)ymax=
;(Ⅱ)ymax=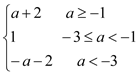
【解析】试题分析:(Ⅰ)分类讨论,由![]() 恰有一解及
恰有一解及![]() 有两个不同的解求得;
有两个不同的解求得;
(Ⅱ)分类讨论,从而确定二次函数的单调性及最值,从而确定函数![]() 在
在![]() 上的最大值.
上的最大值.
试题解析:(Ⅰ)由题意得:
![]()
2![]() 有两个不同的解,且其中一解x=2;
有两个不同的解,且其中一解x=2;
![]()
![]()
综上所述: ![]()
(Ⅱ)(1)若![]() ≤0,即a≥0时,
≤0,即a≥0时,
函数y=|f(x)|在[0,1]上单调递增,
故ymax=f(1)=2+a;
(2)若0<![]() <1,即-2<a<0时,
<1,即-2<a<0时,
此时△=a2-4<0,且f(x)的图象的对称轴在(0,1)上,且开口向上;
故ymax=max{f(0),f(1)}=max{1,a+2}=![]()
(3)若![]() ≥1,即a≤-2时,
≥1,即a≤-2时,
此时f(1)=2+a≤0,
ymax=max{f(0),-f(1)}=max{1,-a-2}=![]()
综上所述,ymax=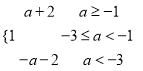


科目:高中数学 来源: 题型:
【题目】设函数f(x)=log2x-![]() (0<x<1),数列{an}满足f(2an)=2n(n∈N*).
(0<x<1),数列{an}满足f(2an)=2n(n∈N*).
(1) 求数列{an}的通项公式;
(2) 判断数列{an}的单调性.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司在迎新年晚会上举行抽奖活动,有甲、乙两个抽奖方案供员工选择;
方案甲:员工最多有两次抽奖机会,每次抽奖的中奖率为![]() .第一次抽奖,若未中奖,则抽奖结束.若中奖,则通过抛一枚质地均匀的硬币,决定是否继续进行第二次抽奖,规定:若抛出硬币,反面朝上,员工则获得500元奖金,不进行第二次抽奖;若正面朝上,员工则须进行第二次抽奖,且在第二次抽奖中,若中奖,获得奖金1000元;若未中奖,则所获奖金为0元.
.第一次抽奖,若未中奖,则抽奖结束.若中奖,则通过抛一枚质地均匀的硬币,决定是否继续进行第二次抽奖,规定:若抛出硬币,反面朝上,员工则获得500元奖金,不进行第二次抽奖;若正面朝上,员工则须进行第二次抽奖,且在第二次抽奖中,若中奖,获得奖金1000元;若未中奖,则所获奖金为0元.
方案乙:员工连续三次抽奖,每次中奖率均为![]() ,每次中奖均可获奖金400元.
,每次中奖均可获奖金400元.
(1)求某员工选择方案甲进行抽奖所获奖金![]() (元)的分布列;
(元)的分布列;
(2)某员工选择方案乙与选择方案甲进行抽奖,试比较哪个方案更划算?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解篮球爱好者小李的投篮命中率与打篮球时间之间的关系,下表记录了小李某月1号到5号每天打篮球时间![]() (单位:小时)与当天投篮命中率
(单位:小时)与当天投篮命中率![]() 之间的关系:
之间的关系:
时间 | 1 | 2 | 3 | 4 | 5 |
命中率 | 0.4 | 0.5 | 0.6 | 0.6 | 0.4 |
小李这5天的平均投篮命中率;用线性回归分析的方法,预测小李该月6号打6小时篮球的投篮命中率.
附:线性回归方程![]() 中系数计算公式
中系数计算公式 ,
, ![]() ,
,
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C的中心在原点,一个焦点为![]() ,且长轴与短轴长的比是
,且长轴与短轴长的比是![]()
(1)求椭圆C的方程;
(2)设点![]() 在 椭圆C的长轴上,点P是椭圆上任意一点,当
在 椭圆C的长轴上,点P是椭圆上任意一点,当![]() 最小时,点P恰好落在椭圆的右顶点上,求实数
最小时,点P恰好落在椭圆的右顶点上,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题12分)根据国家环保部新修订的《环境空气质量标准》规定:居民区PM2.5的年平均浓度不得超过35微克/立方米,PM2.5的24小时平均浓度不得超过75微克/立方米.某城市环保部门随机抽取了一居民区去年20天PM2.5的24小时平均浓度的监测数据,数据统计如下:
]
组别 | PM2.5浓度(微克/立方米) | 频数(天) | 频率 |
第一组 |
| 3 | 0.15 |
第二组 |
| 12 | 0.6 |
第三组 |
| 3 | 0.15 |
第四组 |
| 2 | 0.1 |
(Ⅰ)从样本中PM2.5的24小时平均浓度超过50微克/立方米的5天中,随机抽取2天,求恰好有一天PM2.5的24小时平均浓度超过75微克/立方米的概率;
(Ⅱ)求样本平均数,并根据样本估计总体的思想,从PM2.5的年平均浓度考虑,判断该居民区的环境是否需要改进?说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com