
【题目】已知数列{an}中,a1=2,a2=6,且数列{an﹣1﹣an}{n∈N*}是公差为2的等差数列.
(1)求{an}的通项公式;
(2)记数列{ ![]() }的前n项和为Sn , 求满足不等式Sn>
}的前n项和为Sn , 求满足不等式Sn> ![]() 的n的最小值.
的n的最小值.
【答案】
(1)解:数列 ![]() 是首项为a2﹣a1=4,公差为2的等差数列,
是首项为a2﹣a1=4,公差为2的等差数列,
∴an+1﹣an=4+2(n﹣1)=2n+2(n∈N*).
∴an=a1+(a2﹣a1)+(a3﹣a2)+…+(an﹣an﹣1)=2+4+6+…+2n=n2+n.
(2)解: ![]() ,
,
∴ ![]() =
= ![]() ,
,
由 ![]() 得
得 ![]() ,n>2015,
,n>2015,
又n∈N*,故n的最小值为2016.
【解析】(1)利用等差数列的通项公式及其“累加求和”方法即可得出;(2)利用“裂项求和”方法、不等式的解法即可得出.
【考点精析】认真审题,首先需要了解数列的前n项和(数列{an}的前n项和sn与通项an的关系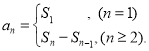 ),还要掌握数列的通项公式(如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式)的相关知识才是答题的关键.
),还要掌握数列的通项公式(如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式)的相关知识才是答题的关键.


 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案科目:高中数学 来源: 题型:
【题目】如图,以坐标原点O为圆心的单位圆与x轴正半轴相交于点A,点B、P在单位圆上,且B(﹣ ![]() ,
, ![]() ),∠AOB=α.
),∠AOB=α. 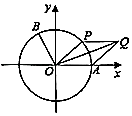
(1)求 ![]() 的值;
的值;
(2)设∠AOP=θ( ![]() ≤θ≤
≤θ≤ ![]() ),
), ![]() =
= ![]() +
+ ![]() ,四边形OAQP的面积为S,f(θ)=(
,四边形OAQP的面积为S,f(θ)=( ![]()
![]() ﹣
﹣ ![]() )2+2S2﹣
)2+2S2﹣ ![]() ,求f(θ)的最值及此时θ的值.
,求f(θ)的最值及此时θ的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列各组中的函数f(x),g(x)表示同一函数的是( )
A.f(x)=x,g(x)= ![]()
B.f(x)=x+1,g(x)= ![]()
C.f(x)=|x|,g(x)= ![]()
D.f(x)=log22x , g(x)=2log2x
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】大学生村官王善良落实政府“精准扶贫”精神,帮助贫困户张三用9万元购进一部节能环保汽车,用于出租.假设第一年需运营费用2万元,从第二年起,每年运营费用均比上一年增加2万元,该车每年的运营收入均为11万元.若该车使用了n(n∈N*)年后,年平均盈利额达到最大值,则n等于(注:年平盈利额=(总收入﹣总成本)× ![]() )( )
)( )
A.3
B.4
C.5
D.6
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=( ![]() )x的图象与函数y=g(x)的图象关于直线y=x对称.
)x的图象与函数y=g(x)的图象关于直线y=x对称.
(1)若f(g(x))=6﹣x2 , 求实数x的值;
(2)若函数y=g(f(x2))的定义域为[m,n](m≥0),值域为[2m,2n],求实数m,n的值;
(3)当x∈[﹣1,1]时,求函数y=[f(x)]2﹣2af(x)+3的最小值h(a).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com