
(1) 求p和q的值;
(2) (2)问最少几分钟,甲、乙两人相遇?并求最短时间内可以相遇的概率.
 天天练口算系列答案
天天练口算系列答案科目:高中数学 来源: 题型:044
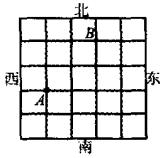
如图所示是一方格迷宫,甲、乙两人分别位于迷宫的A、B两处,两人以每分钟一格的速度同时出发,在每个路口可能向东、西、南、北四个方向行走,已知甲向东、西行走的概率都为![]() ,向南、北行走的概率为
,向南、北行走的概率为![]() 和p,乙向东、西、南、北四个方向行走的概率均为q.
和p,乙向东、西、南、北四个方向行走的概率均为q.
(1) 求p和q的值;
(2) (2)问最少几分钟,甲、乙两人相遇?并求最短时间内可以相遇的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
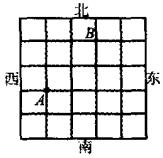
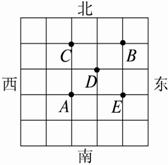
(1)求P和Q的值;
(2)设至少经过t分钟,甲、乙两人能首次相遇,试确定t的值,并求t分钟时,甲、乙两人相遇的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com