分析:(Ⅰ)先根据M在抛物线C
2上,求出抛物线方程,进而得到C
2在点M处的切线方程求出右焦点F的坐标,再结合M在椭圆C
1上即可求出椭圆C
1的标准方程;
(II)先设M
(x0,x0 2),由
y=x2得
y′=x,进而得到C
2在点M处的切线方程求出右焦点F的坐标;再结合M在椭圆C
1上以及p>0求出a,b之间的关系即可得到椭圆C
1离心率的取值范围.
解答: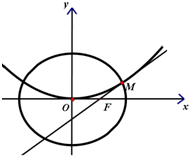
解:(Ⅰ)把M
(2,)代入C
2:x
2=2py(p>0)得
p=,
故C
2:
x2=2y(2分)
由
y=x2得
y′=x,从而C
2在点M处的切线方程为
y-=(x-2)(3分)
令y=0有x=1,F(1,0),(4分)
又M
(2,)在椭圆C
1上
所以
,解得a
2=5,b
2=4,故C
1:
+=1(6分)
(Ⅱ)设M
(x0,x0 2),由
y=x2得
y′=x,
从而C
2在点M处的切线方程为
y-=(x-x0)(8分)
设F(c,0),代入上式得x
0=2c,
因为
+=1,
所以
y02=b2(1-)=b2(1-)=(4b2-3a2)(10分)
又x
02=2py
0,所以
p===,(11分)
从而4b
2>3a
2,即4c
2<a
2,
e2<,
e<,
所以椭圆C
1离心率的取值范围为
0<e<.(13分)
点评:本题主要考查直线与圆锥曲线的综合问题.其中涉及到抛物线以及椭圆标准方程的求法,考查了基本的分析问题的能力和基础的运算能力.

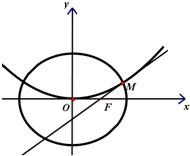 椭圆C1:
椭圆C1: 解:(Ⅰ)把M(2,
解:(Ⅰ)把M(2,

 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案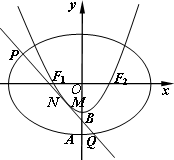 设椭圆C1:
设椭圆C1: