
【题目】已知函数![]() .
.
(Ⅰ)求曲线![]() 在点处的切线方程;
在点处的切线方程;
(Ⅱ)当![]() 时,求证:函数
时,求证:函数![]() 有且仅有一个零点;
有且仅有一个零点;
(Ⅲ)当![]() 时,写出函数
时,写出函数![]() 的零点的个数.(只需写出结论)
的零点的个数.(只需写出结论)
【答案】(Ⅰ)![]() ;(Ⅱ)证明见解析;(Ⅲ)当
;(Ⅱ)证明见解析;(Ⅲ)当![]() 时,
时, ![]() 有一个零点;当
有一个零点;当![]() 且
且![]() 时,
时, ![]() 有两个零点.
有两个零点.
【解析】试题分析:(Ⅰ)求得函数的导函数,得到![]() ,
, ![]() ,进而得到切线的方程.
,进而得到切线的方程.
(Ⅱ)当![]() 时,求得函数
时,求得函数![]() 的导数,得
的导数,得![]() ,则
,则![]() 为单调递增函数,又由
为单调递增函数,又由![]() ,进而得到
,进而得到![]() 在
在![]() 单调递减,在
单调递减,在![]() 单调递增,所以函数
单调递增,所以函数![]() 的最小值为
的最小值为![]() ,即可证明结论;
,即可证明结论;
(Ⅲ)根据函数的单调性和极值,可得当![]() 和
和![]() 且
且![]() 时时,
时时, ![]() 零点的个数.
零点的个数.
试题解析:
(Ⅰ)因为函数![]() ,所以
,所以![]()
故![]() ,
, ![]() , 曲线
, 曲线![]() 在
在![]() 处的切线方程为
处的切线方程为![]()
(Ⅱ)当![]() 时,令
时,令![]() ,则
,则![]()
故![]() 是
是![]() 上的增函数.
上的增函数.
由![]() ,故当
,故当![]() 时,
时, ![]() ,当
,当![]() 时,
时, ![]() .
.
即当![]() 时,
时, ![]() ,当
,当![]() 时,
时, ![]() .
.
故![]() 在
在![]() 单调递减,在
单调递减,在![]() 单调递增.
单调递增.
函数![]() 的最小值为
的最小值为![]() ,由
,由![]() ,故
,故![]() 有且仅有一个零点.
有且仅有一个零点.
(Ⅲ)当![]() 时,
时, ![]() 有一个零点;当
有一个零点;当![]() 且
且![]() 时,
时, ![]() 有两个零点.
有两个零点.


科目:高中数学 来源: 题型:
【题目】如图1, 在直角梯形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 为线段
为线段![]() 的中点. 将
的中点. 将![]() 沿
沿![]() 折起,使平面
折起,使平面![]()
![]() 平面
平面![]() ,得到几何体
,得到几何体![]() ,如图2所示.
,如图2所示.
(1)求证: ![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在“新零售”模式的背景下,某大型零售公司为推广线下分店,计划在![]() 市的
市的![]() 区开设分店.为了确定在该区开设分店的个数,该公司对该市已开设分店的其他区的数据作了初步处理后得到下列表格.记
区开设分店.为了确定在该区开设分店的个数,该公司对该市已开设分店的其他区的数据作了初步处理后得到下列表格.记![]() 表示在各区开设分店的个数,
表示在各区开设分店的个数, ![]() 表示这
表示这![]() 个分店的年收入之和.
个分店的年收入之和.
| 2 | 3 | 4 | 5 | 6 |
| 2.5 | 3 | 4 | 4.5 | 6 |
(Ⅰ)该公司已经过初步判断,可用线性回归模型拟合![]() 与
与![]() 的关系,求
的关系,求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(Ⅱ)假设该公司在![]() 区获得的总年利润
区获得的总年利润![]() (单位:百万元)与
(单位:百万元)与![]() 之间的关系为
之间的关系为![]() ,请结合(Ⅰ)中的线性回归方程,估算该公司应在
,请结合(Ⅰ)中的线性回归方程,估算该公司应在![]() 区开设多少个分店,才能使
区开设多少个分店,才能使![]() 区平均每个分店的年利润最大?
区平均每个分店的年利润最大?
参考公式:
![]() ,
, 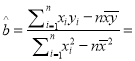
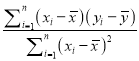 ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来我国电子商务行业迎来发展的新机遇,2017年双11全天交易额达到1682亿元,为规范和评估该行业的情况,相关管理部门制定出针对电商的商品和服务的评价体系.现从评价系统中选出200次成功交易,并对其评价进行评价,对商品的好评率为0.6,对服务的好评率为0.75,其中对商品和服务都做出好评的交易为80次.
(1)完成关于商品和服务评价的![]() 列联表,判断能否在犯错误的概率不超过0.001的前提下,认为商品好评与服务好评有关?
列联表,判断能否在犯错误的概率不超过0.001的前提下,认为商品好评与服务好评有关?
(2)若将频率视为概率,某人在该购物平台上进行的3次购物中,设对商品和服务全为好评的次数为随机变量![]() :
:
①求对商品和服务全为好评的次数![]() 的分布列;
的分布列;
②求![]() 的数学期望和方差.
的数学期望和方差.
附:临界值表:

![]() 的观测值:
的观测值: 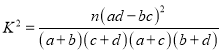 (其中
(其中![]() )
)
关于商品和服务评价的![]() 列联表:
列联表:

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2017·黄冈质检)设等比数列{an}的各项均为正数,公比为q,前n项和为Sn.若对任意的n∈N*,有S2n<3Sn,则q的取值范围是( )
A. (0,1] B. (0,2)
C. [1,2) D. (0, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学调查了某班全部![]() 名同学参加书法社团和演讲社团的情况,数据如下表:(单位:人)
名同学参加书法社团和演讲社团的情况,数据如下表:(单位:人)

(1)能否由![]() 的把握认为参加书法社团和参加演讲社团有关?
的把握认为参加书法社团和参加演讲社团有关?
(附: 
当![]() 时,有
时,有![]() 的把握说事件
的把握说事件![]() 与
与![]() 有关;当
有关;当![]() ,认为事件
,认为事件![]() 与
与![]() 是无关的)
是无关的)
(2)已知既参加书法社团又参加演讲社团的![]() 名同学中,有
名同学中,有![]() 名男同学
名男同学![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 名女同学
名女同学![]() ,
, ![]() ,
, ![]() .现从这
.现从这![]() 名男同学和
名男同学和![]() 名女同学中各随机选
名女同学中各随机选![]() 人,求
人,求![]() 被选中且
被选中且![]() 未被选中的概率.
未被选中的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com