
分析 三个空间向量共面,其充要条件为由它们组成的三阶行列式的值为零.
解答 解:∵$\overline a=(2\;,\;\;-1\;,\;\;3)$,$\overline b=(-1\;,\;\;4\;,\;\;-2)$,$\overline c=(7\;,\;\;5\;,\;\;λ)$.$\overline a$,$\overline b$,$\overline c$共面,
∴$|\begin{array}{l}{2}&{-1}&{3}\\{-1}&{4}&{-2}\\{7}&{5}&{λ}\end{array}|$=8λ-15+14-84+20-λ=0,
解得λ=$\frac{65}{7}$,∴$\overrightarrow{c}$=(7,5,$\frac{65}{7}$),
∴$\overline c$在$\overline a$上的投影为:|$\overrightarrow{c}$|cos<$\overrightarrow{a},\overrightarrow{c}$>=$\frac{\overrightarrow{a}•\overrightarrow{c}}{|\overrightarrow{a}|}$=$\frac{14-5+\frac{195}{7}}{\sqrt{4+1+9}}$=$\frac{18\sqrt{14}}{7}$.
故答案为:$\frac{18\sqrt{14}}{7}$.
点评 本题考查一个向量在另一个向量上的投影的求法,是基础题,解题时要认真审题,注意向量共面的性质的合理运用.


科目:高中数学 来源: 题型:解答题
 如图,在四棱锥C-ABDE中,F为CD的中点,BD⊥平面ABC,BD∥AE且BD=2AE.
如图,在四棱锥C-ABDE中,F为CD的中点,BD⊥平面ABC,BD∥AE且BD=2AE.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在直三棱柱ABC-A1B1C1中,底面ABC为等边三角形,CC1=2AC=2.
如图,在直三棱柱ABC-A1B1C1中,底面ABC为等边三角形,CC1=2AC=2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
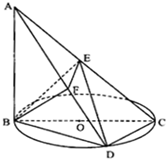 如图,BC为圆O的直径,D为圆周上异于B、C的一点,AB垂直于圆O所在的平面,BE⊥AC于点E,BF⊥AD于点F.
如图,BC为圆O的直径,D为圆周上异于B、C的一点,AB垂直于圆O所在的平面,BE⊥AC于点E,BF⊥AD于点F.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=1,y=$\frac{x}{x}$ | B. | y=$\sqrt{x-2}$•$\sqrt{x+2}$,y=$\sqrt{{x}^{2}-4}$ | ||
| C. | y=x与y=logaax(a>0且a≠1) | D. | y=|x|,$y={({\sqrt{x}})^2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com