
| 1 |
| bnbn+1 |
| n-1 |
| 2 |
| 1 |
| bn |
| 2 |
| n-1 |
| 1 |
| bnbn+1 |
| 4 |
| (n-1)n |
| 1 |
| n-1 |
| 1 |
| n |
| 2 |
| 2 |
| n-1 |
| 2 |
| n-1 |
| 2 |
| 1 |
| bn |
| 2 |
| n-1 |
| 1 |
| bnbn+1 |
| 4 |
| (n-1)n |
| 1 |
| n-1 |
| 1 |
| n |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n-1 |
| 1 |
| n |
| 1 |
| n |
| 4(n-1) |
| n |


科目:高中数学 来源: 题型:
|
|
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
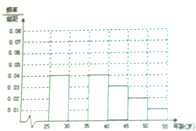 某班同学利用五一劳动节进行社会实践,对信宜城区[25,55]岁的人群随机抽取n人进行生活习惯是否符合低碳观念的调查.得到如图所示的人数频率分布直方图,若生活习惯符合低碳观念,则称为“低碳族”,否则称为“非低碳族”,得到如图所示的人数统计表.
某班同学利用五一劳动节进行社会实践,对信宜城区[25,55]岁的人群随机抽取n人进行生活习惯是否符合低碳观念的调查.得到如图所示的人数频率分布直方图,若生活习惯符合低碳观念,则称为“低碳族”,否则称为“非低碳族”,得到如图所示的人数统计表.| 组数 | 分组 | 低碳族的人数 | 占本组的频率 |
| 第一组 | [25,30﹚ | 120 | 0.6 |
| 第二组 | [30,35﹚ | 195 | p |
| 第三组 | [35,40﹚ | 100 | 0.5 |
| 第四组 | [40,45﹚ | a | 0.4 |
| 第五组 | [45,50﹚ | 30 | 0.3 |
| 第六组 | [50,55] | 15 | 0.3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
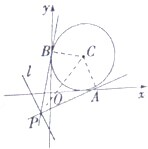 已知P是直线l:3x+4y+8=0上的动点,PA,PB是圆C:x2+y2-2x-2y+1=0的两条切线,A、B是切点.
已知P是直线l:3x+4y+8=0上的动点,PA,PB是圆C:x2+y2-2x-2y+1=0的两条切线,A、B是切点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com