
分析 令t=$\frac{4}{3}$x-sinx,利用单调性求函数t的值域,再利用正弦函数的定义域和值域求得f(x)=sint 的值域.
解答 解:令t=$\frac{4}{3}$x-sinx,由于t′=$\frac{4}{3}$-cosx在[0,π]上的大于零,故函数t在[0,π]上单调递增,
故t∈[0,$\frac{4π}{3}$],故函数f(x)=sin($\frac{4}{3}$x-sinx)=sint 的值域为[-$\frac{\sqrt{3}}{2}$,1],
故答案为:[-$\frac{\sqrt{3}}{2}$,1].
点评 本题主要考查利用导数研究函数的单调性,利用单调性求函数的值域,正弦函数的定义域和值域,属于中档题.


科目:高中数学 来源: 题型:解答题
| 第1次 | 第2次 | 第3次 | 第4次 | 第5次 | |
| 甲 | 59 | 62 | 76 | 80 | 88 |
| 乙 | 56 | 66 | 76 | 78 | 89 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\frac{1}{2}$,1) | B. | (1,2) | C. | (1,2] | D. | ($\frac{1}{2}$,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
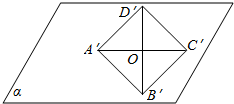 在水平放置的平面α内有一个边长为1的正方形A′B′C′D′.如图,其中的对角线A′C′在水平位置,已知该正方形是某个四边形用斜二测画法画出的直观图,试画出该四边形的真实图形并求出其面积.
在水平放置的平面α内有一个边长为1的正方形A′B′C′D′.如图,其中的对角线A′C′在水平位置,已知该正方形是某个四边形用斜二测画法画出的直观图,试画出该四边形的真实图形并求出其面积.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com