
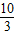 )与抛物线y2=2x上的点P的距离为d1,P到抛物线准线l的距离为d2,则d1+d2取最小值时,P点的坐标为( )
)与抛物线y2=2x上的点P的距离为d1,P到抛物线准线l的距离为d2,则d1+d2取最小值时,P点的坐标为( )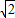 )
)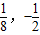 )
)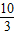 )在抛物线y2=2x的外部然后做出图形(如下图)则PM=d1过p作PN⊥直线x=
)在抛物线y2=2x的外部然后做出图形(如下图)则PM=d1过p作PN⊥直线x= 则PN=d2,根据抛物线的定义可得d1+d2=PM+PF故要使d1+d2取最小值则只有当P,M,F三点共线时成立因此可求出MF所在的直线方程然后与抛物线的方程联立即可求出P点的坐标.
则PN=d2,根据抛物线的定义可得d1+d2=PM+PF故要使d1+d2取最小值则只有当P,M,F三点共线时成立因此可求出MF所在的直线方程然后与抛物线的方程联立即可求出P点的坐标.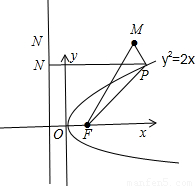 解:∵(3,
解:∵(3,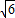 )在抛物线y2=2x上且
)在抛物线y2=2x上且
 )在抛物线y2=2x的外部
)在抛物线y2=2x的外部 ,0),准线方程为x=-
,0),准线方程为x=-
 则PN=d2,
则PN=d2,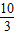 =
= (x-3)即4x-3y-2=0
(x-3)即4x-3y-2=0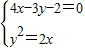 则
则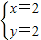 即当点的坐标为(2,2)时d1+d2取最小值
即当点的坐标为(2,2)时d1+d2取最小值

 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:高中数学 来源:2014届河南灵宝第三高级中学高二上学期第三次质量检测理数学(解析版) 题型:选择题
设定点M(3,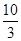 )与抛物线
)与抛物线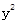 =2x上的点P的距离为
=2x上的点P的距离为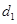 ,P到抛物线准线l的距为
,P到抛物线准线l的距为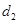 ,则
,则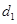 +
+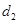 取最小值时,P点的坐标为
取最小值时,P点的坐标为
A.(0,0) B.(1,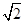 ) C.(2,2) D.(
) C.(2,2) D.( ,-
,-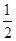 )
)
查看答案和解析>>
科目:高中数学 来源:2012-2013学年河北省保定市高二(上)期末数学试卷(理科)(解析版) 题型:选择题
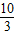 )与抛物线y2=2x上的点P的距离为d1,P到抛物线准线l的距离为d2,则d1+d2取最小值时,P点的坐标为( )
)与抛物线y2=2x上的点P的距离为d1,P到抛物线准线l的距离为d2,则d1+d2取最小值时,P点的坐标为( )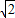 )
)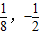 )
)查看答案和解析>>
科目:高中数学 来源:2011-2012学年河北省保定市八校联合体高二(上)期末数学试卷(理科)(解析版) 题型:选择题
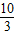 )与抛物线y2=2x上的点P的距离为d1,P到抛物线准线l的距离为d2,则d1+d2取最小值时,P点的坐标为( )
)与抛物线y2=2x上的点P的距离为d1,P到抛物线准线l的距离为d2,则d1+d2取最小值时,P点的坐标为( )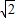 )
)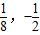 )
)查看答案和解析>>
科目:高中数学 来源:2010年广东省广州一中高三数学二轮复习:圆锥曲线(解析版) 题型:选择题
 )与抛物线y2=2x上的点P的距离为d1,P到抛物线准线l的距离为d2,则d1+d2取最小值时,P点的坐标为( )
)与抛物线y2=2x上的点P的距离为d1,P到抛物线准线l的距离为d2,则d1+d2取最小值时,P点的坐标为( ) )
) )
)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com