【答案】
分析:(I)由Q
n(x
n,y
n),Q
n+1(x
n+1,y
n+1),知点P
n的坐标为(x
n,y
n+1),由此能求出点Q
1、Q
2的坐标;
(II)由Q
n,Q
n+1在曲线C上,知
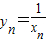
,
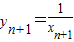
,由P
n在曲线C
n上,知
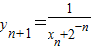
,由此能求出数列{a
n} 的通项公式;
(III)由x
n=(x
n-x
n-1)+(x
n-1-x
n-2)+…+(x
2-x
1)+x
1=2
-(n-1)+2
-(n-2)+…+2
-1+1=
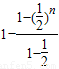
=2-2
1-n,知a
n•b
n=(x
n+1-x
n)•(y
n-y
n+1)=
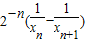
=
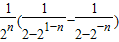
=
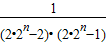
,由此入手能够证明s
n<

.
解答:(I)解:∵Q
n(x
n,y
n),Q
n+1(x
n+1,y
n+1),
∴点P
n的坐标为(x
n,y
n+1)
∵x
1=1∴y
1=1,∴Q
1(x
1,y
1)即Q
1(1,1)
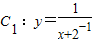
,令x=1则y
2=

∴P
1的坐标为(x
1,y
2)即(1,

)
令

=

得x
2=

∴Q
2(x
2,y
2)即Q
1(

,

).-----------------------------------(2分)
(II)解:∵Q
n,Q
n+1在曲线C上,
∴
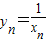
,
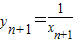
,
又∵P
n在曲线C
n上,
∴
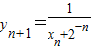
,--------------------------------(4分)
∴x
n+1=x
n+2
-n,
∴a
n=2
-n.-----------------------------------------(6分)
(III)证明:x
n=(x
n-x
n-1)+(x
n-1-x
n-2)+…+(x
2-x
1)+x
1=2
-(n-1)+2
-(n-2)+…+2
-1+1
=
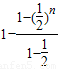
=2-2
1-n.-------------------(9分)
∴a
n•b
n=(x
n+1-x
n)•(y
n-y
n+1)=
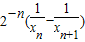
=
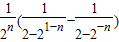
=
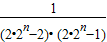
,
∵2•2
n-2≥2
n,2•2
n-1≥3,
∴
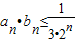
.--------------------------------(12分)
∴S
n=a
1b
1+a
2b
2+…+a
nb
n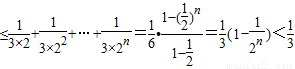
-----------------------(14分)
点评:本题主要考查了等比数列的通项公式,以及等比数列的求和公式和数列与不等式的综合,同时考查了转化的思想和计算的能力,属于难题.

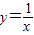 ,
,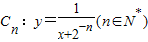 .从C上的点Qn(xn,yn)作x轴的垂线,交Cn于点Pn,再从点Pn作y轴的垂线,交C于点Qn+1(xn+1,yn+1),设x1=1,an=xn+1-xn,bn=yn-yn+1.
.从C上的点Qn(xn,yn)作x轴的垂线,交Cn于点Pn,再从点Pn作y轴的垂线,交C于点Qn+1(xn+1,yn+1),设x1=1,an=xn+1-xn,bn=yn-yn+1. .
.
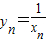 ,
,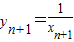 ,由Pn在曲线Cn上,知
,由Pn在曲线Cn上,知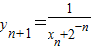 ,由此能求出数列{an} 的通项公式;
,由此能求出数列{an} 的通项公式;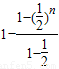 =2-21-n,知an•bn=(xn+1-xn)•(yn-yn+1)=
=2-21-n,知an•bn=(xn+1-xn)•(yn-yn+1)=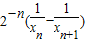 =
=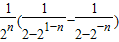 =
=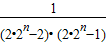 ,由此入手能够证明sn<
,由此入手能够证明sn< .
.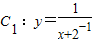 ,令x=1则y2=
,令x=1则y2=
 )
) =
= 得x2=
得x2=
 ,
, ).-----------------------------------(2分)
).-----------------------------------(2分)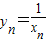 ,
,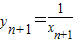 ,
,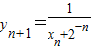 ,--------------------------------(4分)
,--------------------------------(4分)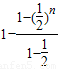
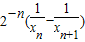 =
=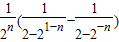 =
=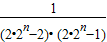 ,
,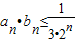 .--------------------------------(12分)
.--------------------------------(12分)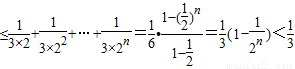 -----------------------(14分)
-----------------------(14分)

 如图,已知曲线C:y=
如图,已知曲线C:y=
 如图,已知曲线C:y=
如图,已知曲线C:y= (2006•南京二模)如图,已知曲线C:y=
(2006•南京二模)如图,已知曲线C:y=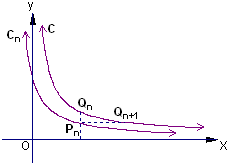 如图,已知曲线C:y=
如图,已知曲线C:y= 如图,已知曲线C:y=x2(0≤x≤1),O(0,0),Q(1,0),R(1,1).取线段OQ的中点A1,过A1作x轴的垂线交曲线C于P1,过P1作y轴的垂线交RQ于B1,记a1为矩形A1P1B1Q的面积.分别取线段OA1,P1B1的中点A2,A3,过A2,A3分别作x轴的垂线交曲线C于P2,P3,过P2,P3分别作y 轴的垂线交A1P1,RB1于B2,B3,记a2为两个矩形A2P2B2A1与矩形A3P3B3B1的面积之和.以此类推,记an为2n-1个矩形面积之和,从而得数列{an},设这个数列的前n项和为Sn.
如图,已知曲线C:y=x2(0≤x≤1),O(0,0),Q(1,0),R(1,1).取线段OQ的中点A1,过A1作x轴的垂线交曲线C于P1,过P1作y轴的垂线交RQ于B1,记a1为矩形A1P1B1Q的面积.分别取线段OA1,P1B1的中点A2,A3,过A2,A3分别作x轴的垂线交曲线C于P2,P3,过P2,P3分别作y 轴的垂线交A1P1,RB1于B2,B3,记a2为两个矩形A2P2B2A1与矩形A3P3B3B1的面积之和.以此类推,记an为2n-1个矩形面积之和,从而得数列{an},设这个数列的前n项和为Sn.