练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】如图C，D是以AB为直径的圆上的两点，，，F是AB上的一点，且，面ABD，．

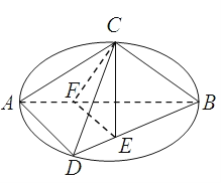
    （1）求证：平面；

    （2）求证：平面；

    （3）求三棱锥的体积．

    【答案】（1）证明见解析；（2）证明见解析；（3）.

    【解析】

    （1）由圆的性质知，由线面垂直性质知；根据线面垂直的判定定理可证得结论；

    （2）根据圆的性质知，由勾股定理可求得；由线面垂直性质知，由勾股定理求得，从而可得到，证得；根据线面平行判定定理证得结论；

    （3）根据比例关系可知，由线面垂直知为点到平面的距离；由体积桥可知，利用三棱锥体积公式求得结果.

    （1）在以为直径的圆上

    平面，平面

    平面， 平面

    （2）在以为直径的圆上 ，又，

    平面，平面 ，又

    在中，

    平面，平面 平面

    （3）

    平面 到平面距离为：

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】 如图是正方体的平面展开图．在这个正方体中，

    ①BM∥平面DE；②CN∥平面AF；③平面BDM∥平面AFN；④平面BDE∥平面NCF.

    以上四个命题中，正确命题的序号是________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数 .

    （1）求函数的极小值；

    （2）求证：当时，.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）若函数的图象在点处的切线方程为，求，的值；

    （2）当时，在区间上至少存在一个，使得成立，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知抛物线y2=2px（p＞0）上点M（3，m）到焦点F的距离为4．

    （Ⅰ）求抛物线方程；

    （Ⅱ）点P为准线上任意一点，AB为抛物线上过焦点的任意一条弦，设直线PA，PB，PF的斜率为k1，k2，k3，问是否存在实数λ，使得k1+k2=λk3恒成立．若存在，请求出λ的值；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在三棱柱中，侧面是矩形，，，，且.

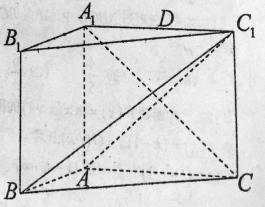
    （1）求证：平面平面；

    （2）设是的中点，判断并证明在线段上是否存在点，使平面，若存在，求点到平面的距离.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在等差数列

    （Ⅰ）求数列的通项公式；

    （Ⅱ）若数列，求数列的前n项和Sn.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某商场为吸引顾客消费推出一项优惠活动．活动规则如下：消费额每满100元可转动如图所示的转盘一次，并获得相应金额的返券，假定指针等可能地停在任一位置.若指针停在A区域返券60元；停在B区域返券30元；停在C区域不返券.例如：消费218元，可转动转盘2次，所获得的返券金额是两次金额之和．

    （1）若某位顾客消费128元，求返券金额不低于30元的概率；

    （2）若某位顾客恰好消费280元，并按规则参与了活动，他获得返券的金额记为（元）．求随机变量的分布列和数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】己知函数，，.

    （1）讨论函数的单调性；

    （2）若在处取得极大值，求的取值范围.

    查看答案和解析>>

    同步练习册答案