
【题目】如图,在四棱锥![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,且
,且![]() ,
,![]() ,
,![]() .
.
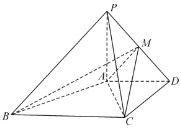
(1)求证:![]() ;
;
(2)在线段![]() 上,是否存在一点
上,是否存在一点![]() ,使得二面角
,使得二面角![]() 的大小为45°,如果存在,求
的大小为45°,如果存在,求![]() 与平面
与平面![]() 所成角的正弦值,如果不存在,请说明理由.
所成角的正弦值,如果不存在,请说明理由.
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案科目:高中数学 来源: 题型:
【题目】已知![]()
![]()
![]() ,若
,若![]() ,且
,且![]() 的图象相邻的对称轴间的距离不小于
的图象相邻的对称轴间的距离不小于![]() .
.
(1)求![]() 的取值范围.
的取值范围.
(2)若当![]() 取最大值时,
取最大值时, ![]() ,且在
,且在![]() 中,
中, ![]() 分别是角
分别是角![]() 的对边,其面积
的对边,其面积![]() ,求
,求![]() 周长的最小值.
周长的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,侧棱
中,侧棱![]() 底面
底面![]() ,底面
,底面![]() 是直角梯形,
是直角梯形,![]() ∥
∥![]() ,
,![]() ,且
,且![]() ,
,![]() ,
,![]() 是棱
是棱![]() 的中点 .
的中点 .
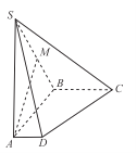
(Ⅰ)求证:![]() ∥平面
∥平面![]() ;
;
(Ⅱ)求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值;
所成锐二面角的余弦值;
(Ⅲ)设点![]() 是线段
是线段![]() 上的动点,
上的动点,![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动圆![]() 过定点
过定点![]() ,并且内切于定圆
,并且内切于定圆![]() .
.
(1)求动圆圆心![]() 的轨迹方程;
的轨迹方程;
(2)若![]() 上存在两个点
上存在两个点![]() ,
,![]() ,(1)中曲线上有两个点
,(1)中曲线上有两个点![]() ,
,![]() ,并且
,并且![]() ,
,![]() ,
,![]() 三点共线,
三点共线,![]() ,
,![]() ,
,![]() 三点共线,
三点共线,![]() ,求四边形
,求四边形![]() 的面积的最小值.
的面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,一座小岛距离海岸线上最近的点P的距离是3 km,从点P沿海岸正东12 km处有一个渔村.
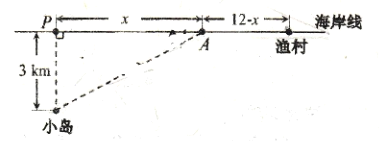
(1)假设一个人驾驶的小船的平均速度为![]() ,步行的速度是
,步行的速度是![]() .y(单位:h)表示他从小岛到渔村的时间,x(单位:km)表示此人将船停在海岸处A与P点的距离.请将y表示为x的函数,并写出定义域;
.y(单位:h)表示他从小岛到渔村的时间,x(单位:km)表示此人将船停在海岸处A与P点的距离.请将y表示为x的函数,并写出定义域;
(2)在(1)的条件下,是否有一个停船的位置使得从小岛到渔村花费的时间最少?说明理由.(![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(12分)已知函数![]() .
.
(1)若x=2是函数f(x)的极值点,求曲线y=f(x)在点(1,f(1))处的切线方程;
(2)若函数f(x)在![]() 上为单调增函数,求a的取值范围;
上为单调增函数,求a的取值范围;
(3)设m,n为正实数,且m>n,求证: ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com