
| A. | y=lg(x+1) | B. | y=tanx | C. | y=2-x | D. | y=x-2 |
分析 根据题意,依次分析选项:对于A、其图象由对数函数y=lgx的图象平移变换得到,分析可得其符合题意,对于B、依据正切函数的定义域,分析可得其定义域不符合题意,对于C、D,均为减函数,不符合题意;综合可得答案.
解答 解:根据题意,依次分析选项:
对于A、函数y=lg(x+1)可以由对数函数y=lgx的图象向左平移1个单位得到,而y=lgx在(0,+∞)是增函数,故函数y=lg(x+1)在(-1,+∞)是增函数,符合题意;
对于B、函数y=tanx的定义域为{x|x≠kπ+$\frac{π}{2}$},在(0,+∞)不是增函数,不符合题意;
对于C、y=2-x=($\frac{1}{2}$)x,为减函数,不符合题意;
对于D、y=x-2=$\frac{1}{{x}^{2}}$,在(0,+∞)是减函数,不符合题意;
故选:A.
点评 本题考查函数的单调性的判断,需要掌握常见函数单调性的性质以及应用,


科目:高中数学 来源: 题型:选择题
| A. | n2 | B. | n(n+1) | C. | $\frac{n(n+1)}{2}$ | D. | (n+1)(n+2) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | -3 | C. | 2 | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{13}$ | B. | $\sqrt{5}$ | C. | $\sqrt{10}$ | D. | 2+$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
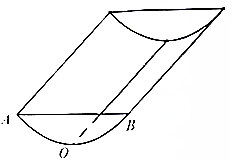 某小区内有一条形状如图的沟渠,沟沿是两条平行线段,沟渠宽AB为20厘米,沟渠的直截面ABO为一段抛物线,抛物线顶点为O,对称轴与地面垂直,沟渠深20厘米,沟渠中水深10厘米.
某小区内有一条形状如图的沟渠,沟沿是两条平行线段,沟渠宽AB为20厘米,沟渠的直截面ABO为一段抛物线,抛物线顶点为O,对称轴与地面垂直,沟渠深20厘米,沟渠中水深10厘米.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {1} | B. | [0,2] | C. | (0,2) | D. | {0,1,2} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com