
| A. | ①② | B. | ①③ | C. | ②③ | D. | ①②③ |
分析 ①求出${∫}_{-a}^{a}$f(x)dx的积分,结合函数的图象得出存在a>0,使${∫}_{-a}^{a}$f(x)dx=0成立;
②求出${∫}_{-a}^{a}$(ex+x)dx=0时a的值,得出命题不成立;
③根据f(x)是定义域上的奇函数,积分的上下限互为相反数,得出定积分值为0,满足条件.
解答 解:对于①,f(x)=xsinx,
∵(sinx-xcosx)′=xsinx,
∴${∫}_{-a}^{a}$xsinxdx=(sinx-xcosx)${|}_{-a}^{a}$=2sina-2acosa,
令2sina-2acosa=0,
∴sina=acosa,
又cosa≠0,∴tana=a;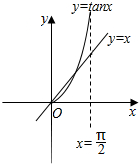
画出函数y=tanx与y=x的部分图象,如图所示;
在(0,$\frac{π}{2}$)内,两函数的图象有交点,
即存在a>0,使${∫}_{-a}^{a}$f(x)dx=0成立,①满足条件;
对于②,f(x)=ex+x,${∫}_{-a}^{a}$(ex+x)dx=(ex+$\frac{1}{2}$x2)${|}_{-a}^{a}$=ea-e-a;
令ea-e-a=0,解得a=0,不满足条件;
对于③,f(x)=ln($\sqrt{1+{x}^{2}}$-x)是定义域R上的奇函数,
且积分的上下限互为相反数,
所以定积分值为0,满足条件;
综上,?a>0,使${∫}_{-a}^{a}$f(x)dx=0的函数是①③.
故选:B.
点评 本题主要考查了定积分运算性质的应用问题,当被积函数为奇函数且积分区间对称时,积分值为0,是综合性题目.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
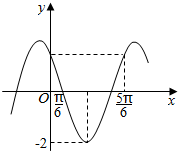 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<2π)的部分图象如图所示,且f(0)=f($\frac{5π}{6}$).
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<2π)的部分图象如图所示,且f(0)=f($\frac{5π}{6}$).查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | -$\sqrt{3}$ | C. | -$\frac{\sqrt{3}}{3}$ | D. | $\frac{\sqrt{3}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2$\sqrt{2}$ | B. | 2$\sqrt{3}$ | C. | $\sqrt{3}$ | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | 4 | D. | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com