
 +
+ =1(a>b>0)的左准线上,过点P且与直线5x+2y=0平行的光线经直线y=-2反射后通过椭圆左焦点,则这个椭圆离心率为( )
=1(a>b>0)的左准线上,过点P且与直线5x+2y=0平行的光线经直线y=-2反射后通过椭圆左焦点,则这个椭圆离心率为( )



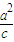 ,点P(-3,1)在椭圆
,点P(-3,1)在椭圆 +
+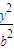 =1(a>b>0)的左准线上.
=1(a>b>0)的左准线上.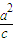 =3,
=3,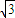 .
.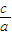 =
=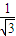 =
=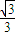 .
.

 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2005•静安区一模)已知等差数列{an}的首项为p,公差为d(d>0).对于不同的自然数n,直线x=an与x轴和指数函数f(x)=(
(2005•静安区一模)已知等差数列{an}的首项为p,公差为d(d>0).对于不同的自然数n,直线x=an与x轴和指数函数f(x)=(| 1 | 2 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| x2 |
| a2 |
| y2 |
| b2 |
A.
| B.
| C.
| D.
|
查看答案和解析>>
科目:高中数学 来源: 题型:
(09年东城区示范校质检一文)点P(―3,―1)在椭圆![]() 的左准线上,过点P且方向向量
的左准线上,过点P且方向向量![]() 的光线,经过直线y=2反射后,通过椭圆的左焦点,则这个椭圆的离心率为 ( )
的光线,经过直线y=2反射后,通过椭圆的左焦点,则这个椭圆的离心率为 ( )
A.![]() B.
B. ![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com