
【题目】已知函数![]()
![]() .
.
(1)当![]() 时,求曲线
时,求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2)当![]() 时,设函数
时,设函数![]() ,且函数
,且函数![]() 有且仅有一个零点,若当
有且仅有一个零点,若当![]() 时,
时, ![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
科目:高中数学 来源: 题型:
【题目】学校计划举办“国学”系列讲座.由于条件限制,按男、女生比例采取分层抽样的方法,从某班选出10人参加活动,在活动前,对所选的10名同学进行了国学素养测试,这10名同学的性别和测试成绩(百分制)的茎叶图如图所示.

(1)分别计算这10名同学中,男女生测试的平均成绩;
(2)若这10名同学中,男生和女生的国学素养测试成绩的标准差分别为S1,S2,试比较S1与S2的大小(不必计算,只需直接写出结果);
(3)规定成绩大于等于75分为优良,从这10名同学中随机选取一男一女两名同学,求这两名同学的国学素养测试成绩均为优良的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=2ax2+2bx,若存在实数x0∈(0,t),使得对任意不为零的实数a,b均有f(x0)=a+b成立,则t的取值范围是_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为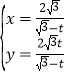 (
(![]() 为参数,且
为参数,且![]() ),以坐标原点为极点,
),以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,已知曲线
轴的正半轴为极轴建立极坐标系,已知曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)将曲线![]() 的参数方程化为普通方程,并将曲线
的参数方程化为普通方程,并将曲线![]() 的极坐标方程化为直角坐标方程;
的极坐标方程化为直角坐标方程;
(2)求曲线![]() 与曲线
与曲线![]() 交点的极坐标
交点的极坐标![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市2016年6月30天的空气质量指数如下:
35 | 54 | 80 | 86 | 72 | 85 | 58 | 125 | 111 | 53 |
10 | 66 | 46 | 36 | 18 | 25 | 23 | 40 | 60 | 89 |
88 | 54 | 79 | 14 | 16 | 40 | 59 | 67 | 111 | 62 |
你觉得这个月的空气质量如何?请设计适当的频率分布直方图展示这组数据,并结合空气质量分级标准分析数据.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 为双曲线
为双曲线![]() 的左、右焦点,过
的左、右焦点,过![]() 作垂直于
作垂直于![]() 轴的直线,在
轴的直线,在![]() 轴上方交双曲线
轴上方交双曲线![]() 于点
于点![]() ,且
,且![]() ,圆
,圆![]() 的方程是
的方程是![]() .
.
(1)求双曲线![]() 的方程;
的方程;
(2)过双曲线![]() 上任意一点
上任意一点![]() 作该双曲线两条渐近线的垂线,垂足分别为
作该双曲线两条渐近线的垂线,垂足分别为![]() ,求
,求![]() 的值;
的值;
(3)过圆![]() 上任意一点
上任意一点![]() 作圆
作圆![]() 的切线
的切线![]() 交双曲线
交双曲线![]() 于
于![]() 两点,
两点, ![]() 中点为
中点为![]() ,
,
求证: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,已知曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数,![]() ).
).
(1)当![]() 时,若曲线
时,若曲线![]() 上存在
上存在![]() 两点关于点
两点关于点![]() 成中心对称,求直线
成中心对称,求直线![]() 的斜率;
的斜率;
(2)在以原点为极点,![]() 轴正半轴为极轴的极坐标系中,极坐标方程为
轴正半轴为极轴的极坐标系中,极坐标方程为![]() 的直线
的直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点,若
两点,若![]() ,求实数
,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 对任意实数
对任意实数![]() ,
,![]() 恒有
恒有![]() ,且当
,且当![]() ,
,![]() ,又
,又![]() .
.
(1)判断![]() 的奇偶性;
的奇偶性;
(2)求![]() 在区间
在区间![]() 上的最大值;
上的最大值;
(3)是否存在实数![]() ,使得不等式
,使得不等式![]() 对一切
对一切![]() 都成立?若存在求出
都成立?若存在求出![]() ;若不存在,请说明理由.
;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某大学数学系图书室中任选一本书,设![]() {数学书},
{数学书},![]() {中文版的书},
{中文版的书},![]() {2018年后出版的书},问:
{2018年后出版的书},问:
(1)![]() 表示什么事件?
表示什么事件?
(2)在什么条件下,有![]() ?
?
(3)![]() 表示什么意思?
表示什么意思?
(4)如果![]() ,那么是否意味着图书室中的所有的数学书都不是中文版的?
,那么是否意味着图书室中的所有的数学书都不是中文版的?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com