
【题目】已知等比数列![]() 中,
中, ![]() ,
, ![]() 成等差数列;数列
成等差数列;数列![]() 中的前
中的前![]() 项和为
项和为![]() ,
, ![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)求数列 的前
的前![]() 项和.
项和.
【答案】(1) ![]() ,
,![]() ;(2)
;(2) ![]() .
.
【解析】试题分析:(1)根据![]() ,
, ![]() 成等差数列列出关于首项
成等差数列列出关于首项![]() ,公比
,公比![]() 的方程组,解得
的方程组,解得![]() 、
、![]() 的值,即可得到数列
的值,即可得到数列![]() 的通项公式,当
的通项公式,当![]() 时,
时, ![]() ,(
,( ![]() 也适合);(2)由(1)知
也适合);(2)由(1)知![]() 根据等比数列的求和公式和裂项相消求和以及分组即可求出数列
根据等比数列的求和公式和裂项相消求和以及分组即可求出数列 的前
的前![]() 项和.
项和.
试题解析:(1)设等比数列![]() 的公比为
的公比为![]() ;
;
因为![]() 成等差数列,故
成等差数列,故
![]() ,
,
即![]() ,故
,故![]() ;
;
因为![]() ,即
,即![]() .
.
因为![]() ,故当
,故当![]() 时,
时, ![]() .
.
当![]() 时,
时, ![]() ;
;
综上所述![]() .
.
(2)由(1)知![]() ;
; ![]()
故数列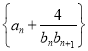 的前
的前![]() 项和为
项和为
 .
.
【方法点晴】本题主要考查等差数列的通项与求和公式,以及裂项相消法求数列的和,属于中档题. 裂项相消法是最难把握的求和方法之一,其原因是有时很难找到裂项的方向,突破这一难点的方法是根据式子的结构特点,常见的裂项技巧:(1) ![]() ;(2)
;(2) ![]()
![]() ; (3)
; (3)![]() ;(4)
;(4)![]()
 ;此外,需注意裂项之后相消的过程中容易出现丢项或多项的问题,导致计算结果错误.
;此外,需注意裂项之后相消的过程中容易出现丢项或多项的问题,导致计算结果错误.


 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:高中数学 来源: 题型:
【题目】某花店每天以每枝5元的价格从农场购进若干枝玫瑰花,然后以每枝10元的价格出售.如果当天卖不完,剩下的玫瑰花作垃圾处理.
(1)若花店一天购进17枝玫瑰花,求当天的利润y(单位:元)关于当天需求量n(单位:枝,n∈N)的函数解析式;
(2)花店记录了100天玫瑰花的日需求量(单位:枝),整理得下表:
日需求量n | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
频数 | 10 | 20 | 16 | 16 | 15 | 13 | 10 |
①假设花店在这100天内每天购进17枝玫瑰花,求这100天的日利润(单位:元)的平均数;
②若花店一天购进17枝玫瑰花,以100天记录的各需求量的频率作为各需求量发生的概率,求当天的利润不少于75元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知曲线
中,已知曲线![]() ,以平面直角坐标系
,以平面直角坐标系![]() 的原点
的原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴,取相同的单位长度建立极坐标系,已知直线
轴的正半轴为极轴,取相同的单位长度建立极坐标系,已知直线![]() .
.
(1)将曲线![]() 上的所有点的横坐标、纵坐标分别伸长为原来的
上的所有点的横坐标、纵坐标分别伸长为原来的![]() 倍、2倍后得到曲线
倍、2倍后得到曲线![]() .试写出直线
.试写出直线![]() 的直角坐标方程和曲线
的直角坐标方程和曲线![]() 的参数方程;
的参数方程;
(2)在曲线![]() 上求一点
上求一点![]() ,使点
,使点![]() 到直线
到直线![]() 的距离最大,并求出此最大值.
的距离最大,并求出此最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,梯形![]() 中,
中, ![]() 为
为![]() 中点.将
中点.将![]() 沿
沿![]() 翻折到
翻折到![]() 的位置,如图2.
的位置,如图2.

(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(Ⅲ)设![]() 分别为
分别为![]() 和
和![]() 的中点,试比较三棱锥
的中点,试比较三棱锥![]() 和三棱锥
和三棱锥![]() (图中未画出)的体积大小,并说明理由.
(图中未画出)的体积大小,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在等腰梯形![]() 中,
中, ![]() ,上底
,上底![]() ,下底
,下底![]() ,点
,点![]() 为下底
为下底![]() 的中点,现将该梯形中的三角形
的中点,现将该梯形中的三角形![]() 沿线段
沿线段![]() 折起,形成四棱锥
折起,形成四棱锥![]() .
.

(1)在四棱锥![]() 中,求证:
中,求证: ![]() ;
;
(2)若平面![]() 与平面
与平面![]() 所成二面角的平面角为
所成二面角的平面角为![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com