Question

【题目】

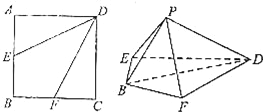
如图，在正方形ABCD中，点E，F分别是AB，BC的中点．将△AED，△DCF分别沿DE，DF折起，使A，C两点重合于P．

（1）求证：平面PBD⊥平面BFDE；

（2）求二面角P﹣DE﹣F的余弦值．

Answer 1

【答案】（1）证明略 （2）

【解析】试题分析：证明面面垂直只需在一个平面内寻求一条直线和另一个平面垂直，本题寻找到直线，先证明垂直平面，然后得出面面垂直；求二面角使用法向量，建立空间直角坐标系，求出两个半平面的法向量，用公式求出二面角的余弦.

试题解析：

证明：（1）由正方形ABCD知，∠DCF=∠DAE=90°，EF∥AC，BD⊥AC，EF⊥BD，

∵点E，F分别是AB，BC的中点．将△AED，△DCF分别沿DE，DF折起，使A，C两点重合于P．

∴PD⊥PF，PD⊥PE，

∵PE∩PF=P，PE、PF平面PEF．

∴PD⊥平面PEF．

又∵EF平面PEF，

∴PD⊥EF，又BD∩PD=D，

∴EF⊥平面PBD，

又EF平面BFDE，∴平面PBD⊥平面BFDE．

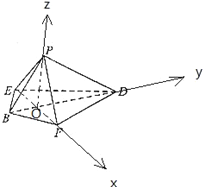
（2）连结BD、EF，交于点O，以O为原点，OF为x轴，OD为y轴，OP为z轴，建立空间直角坐标系，

设在正方形ABCD的边长为2，则DO=， =，PE=PF=1，PO==，

∴P（0，0，），D（0，，0），E（﹣，0，0），F（，0，0），

=（﹣，﹣，0），=（0，﹣，），=（，﹣，0），

设平面PDE的法向量=（x，y，z），

则，取y=1，则=（﹣3，，3），

平面DEF的法向量=（0，0，1），

设二面角P﹣DE﹣F的平面角为θ，

则cosθ===．

∴二面角P﹣DE﹣F的余弦值为．