
【题目】三维柱形图中柱的高度表示的是( )
A. 各分类变量的频数 B. 分类变量的百分比
C. 分类变量的样本数 D. 分类变量的具体值
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin(π﹣ωx)cosωx+cos2ωx(ω>0)的最小正周期为π.
(Ⅰ)求ω的值;
(Ⅱ)将函数y=f(x)的图象上各点的横坐标缩短到原来的![]() ,纵坐标不变,得到函数y=g(x)的图象,求函数y=g(x)在区间
,纵坐标不变,得到函数y=g(x)的图象,求函数y=g(x)在区间![]() 上的最小值.
上的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学校某研究性学习小组在对学生上课注意力集中情况的调查研究中,发现其在40分钟的一节课中,注意力指数![]() 与听课时间
与听课时间![]() (单位:分钟)之间的关系满足如图所示的图象,当
(单位:分钟)之间的关系满足如图所示的图象,当![]() 时,图象是二次函数图象的一部分,其中顶点
时,图象是二次函数图象的一部分,其中顶点![]() ,过点
,过点![]() ;当
;当![]() 时,图象是线段
时,图象是线段![]() ,其中
,其中![]() .根据专家研究,当注意力指数大于62时,学习效果最佳.
.根据专家研究,当注意力指数大于62时,学习效果最佳.
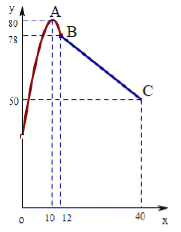
(1)试求![]() 的函数关系式;
的函数关系式;
(2)教师在什么时段内安排内核心内容,能使得学生学习效果最佳?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方体ABCD-A1B1C1D1的棱长为1,P为BC的中点,Q为线段CC1上的动点,过点A,P,Q的平面截该正方体所得的截面记为S,则下列命题正确的是 .(填序号)
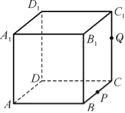
①当0<CQ<![]() 时,S为四边形;
时,S为四边形;
②当CQ=![]() 时,S为等腰梯形;
时,S为等腰梯形;
③当CQ=![]() 时,S与C1D1的交点R满足C1R=
时,S与C1D1的交点R满足C1R=![]() ;
;
④当![]() <CQ<1时,S为六边形;
<CQ<1时,S为六边形;
⑤当CQ=1时,S的面积为![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() 为其导函数,且
为其导函数,且![]() 时
时![]() 有极小值-9.
有极小值-9.
(1)求![]() 的单调递减区间;
的单调递减区间;
(2)若![]() ,
,![]() ,当
,当![]() 时,对于任意
时,对于任意![]() ,
,![]() 和
和![]() 的值至少有一个是正数,求实数
的值至少有一个是正数,求实数![]() 的取值范围;
的取值范围;
(3)若不等式![]() (
(![]() 为正整数)对任意正实数
为正整数)对任意正实数![]() 恒成立,求
恒成立,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国是世界上严重缺水的国家,城市缺水尤为突出.某市为了制定合理的节水方案,从该市随机调查了100位居民,获得了他们某月的用水量,整理得到如图的频率分布直方图.
(1)求图中![]() 的值;
的值;
(2)设该市有500万居民,估计全市居民中月均用水量不低于3吨的人数,说明理由:
(3)估计本市居民的月用水量平均数(同一组中的数据用该区间的中点值代表).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com