
【题目】已知圆C的方程为:x2+y2=4
(1)求过点P(2,1)且与圆C相切的直线l的方程;
(2)直线l过点D(1,2),且与圆C交于A、B两点,若|AB|=2 ![]() ,求直线l的方程;
,求直线l的方程;
(3)圆C上有一动点M(x0 , y0), ![]() =(0,y0),若向量
=(0,y0),若向量 ![]() =
= ![]() +
+ ![]() ,求动点Q的轨迹方程.
,求动点Q的轨迹方程.
【答案】
(1)解:当k不存在时,x=2满足题意;
当k存在时,设切线方程为y﹣1=k(x﹣2),
由 ![]() =2得,k=﹣
=2得,k=﹣ ![]() ,
,
则所求的切线方程为x=2或3x+4y﹣10=0
(2)解:当直线l垂直于x轴时,此时直线方程为x=1,l与圆的两个交点坐标为(1, ![]() )和(1,﹣
)和(1,﹣ ![]() ),这两点的距离为2
),这两点的距离为2 ![]() ,满足题意;
,满足题意;
当直线l不垂直于x轴时,设其方程为y﹣2=k(x﹣1),即kx﹣y﹣k+2=0,
设圆心到此直线的距离为d,
∴d=  =1,即
=1,即 ![]() =1,
=1,
解得:k= ![]() ,
,
此时直线方程为3x﹣4y+5=0,
综上所述,所求直线方程为3x﹣4y+5=0或x=1
(3)解:设Q点的坐标为(x,y),
∵M(x0,y0), ![]() =(0,y0),
=(0,y0), ![]() =
= ![]() +
+ ![]() ,
,
∴(x,y)=(x0,2y0),
∴x=x0,y=2y0,
∵x02+y02=4,
∴x2+( ![]() )2=4,即
)2=4,即 ![]() +
+ ![]() =1
=1
【解析】(1)分两种情况考虑:当直线l的斜率不存在时,直线x=2满足题意;当k存在时,变形出l方程,利用圆心到l的距离d=r列出方程,求出方程的解得到k的值,确定出此时l方程,综上,得到满足题意直线l的方程;(2)分两种情况考虑:当直线l垂直于x轴时,此时直线方程为x=1,直线l与圆的两个交点距离为2 ![]() ,满足题意;
,满足题意;
当直线l不垂直于x轴时,设其方程为y﹣2=k(x﹣1),求出圆心到直线l的距离d=1,利用点到直线的距离公式列出关于k的方程,求出方程的解得到k的值,确定出此时直线方程,综上,得到满足题意直线l的方程;(3)设Q(x,y),表示出 ![]() ,
, ![]() ,代入已知等式中化简得到x=x0 , y=2y0 , 代入圆方程变形即可得到Q轨迹方程.
,代入已知等式中化简得到x=x0 , y=2y0 , 代入圆方程变形即可得到Q轨迹方程.


科目:高中数学 来源: 题型:
【题目】已知等差数列{an}的前n项和为Sn , 且a3=7,a5+a7=26
(1)求an及Sn;
(2)令bn= ![]() (n∈N*)求数列{bn}的前n项和Tn .
(n∈N*)求数列{bn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数y=x+ ![]() (a>0)在区间
(a>0)在区间 ![]() 上单调递减,在区间
上单调递减,在区间 ![]() 上单调递增;函数
上单调递增;函数 ![]()
(1)请写出函数f(x)=x2+ ![]() (a>0)与函数g(x)=xn+
(a>0)与函数g(x)=xn+ ![]() (a>0,n∈N,n≥3)在(0,+∞)的单调区间(只写结论,不证明);
(a>0,n∈N,n≥3)在(0,+∞)的单调区间(只写结论,不证明);
(2)求函数h(x)的最值;
(3)讨论方程h2(x)﹣3mh(x)+2m2=0(0<m≤30)实根的个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= 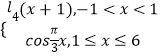 ,若存在实数x1 , x2 , x3 , x4 , 满足x1<x2<x3<x4 , 且f(x1)=f(x2)=f(x3)=f(x4),则
,若存在实数x1 , x2 , x3 , x4 , 满足x1<x2<x3<x4 , 且f(x1)=f(x2)=f(x3)=f(x4),则 ![]() 的取值范围是( ).
的取值范围是( ).
A.(0,4)
B.(0, ![]() )
)
C.( ![]() ,
, ![]() )
)
D.( ![]() ,
, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】正方形ABCD所在的平面与三角形CDE所在的平面交于CD,且AE⊥平面CDE. 
(1)求证:AB∥平面CDE;
(2)求证:平面ABCD⊥平面ADE.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在五面体ABCDEF中,四边形ABCD是边长为2的正方形,EF∥平面ABCD,EF=1,FB=FC,∠BFC=90°,AE= ![]() ,H是BC的中点.
,H是BC的中点. 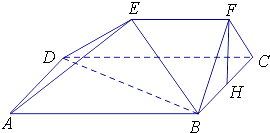
(1)求证:FH∥平面BDE;
(2)求证:AB⊥平面BCF;
(3)求五面体ABCDEF的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
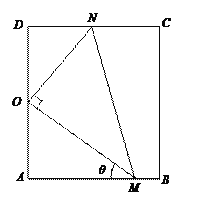
【题目】如图,矩形ABCD是某小区户外活动空地的平面示意图,其中AB=50![]() 米,AD=100米,现拟在直角三角形OMN内栽植草坪供儿童踢球娱乐(其中,点O为AD的中点,OM⊥ON,点M在AB上,点N在CD上),将破旧的道路AM重新铺设.已知草坪成本为每平方米20元,新道路AM成本为每米500元,设∠OMA=θ,记草坪栽植与新道路铺设所需的总费用为f(θ).
米,AD=100米,现拟在直角三角形OMN内栽植草坪供儿童踢球娱乐(其中,点O为AD的中点,OM⊥ON,点M在AB上,点N在CD上),将破旧的道路AM重新铺设.已知草坪成本为每平方米20元,新道路AM成本为每米500元,设∠OMA=θ,记草坪栽植与新道路铺设所需的总费用为f(θ).
(1)求f(θ)关于θ函数关系式,并写出定义域;
(2)为节约投入成本,当tanθ为何值时,总费用 f(θ)最小?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C对应的边分别是a,b,c,已知cos2A﹣3cos(B+C)=1.
(Ⅰ)求角A的大小;
(Ⅱ)若△ABC的面积S=5 ![]() ,b=5,求sinBsinC的值.
,b=5,求sinBsinC的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC,|AB|=8,AC与BC边所在直线的斜率之积为定值m,
(1)求动点C的轨迹方程;
(2)当m=1时,过点E(0,1)的直线l与曲线C相交于P、Q两点,求P、Q两点的中点M的轨迹方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com