练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    在长方体ABCD－A1B1C1D1中，点P为棱AB的中点，且AB＝2，，AD＝1．

    (1)

    求证：AB1⊥平面A1PD1；

    (2)

    求二面角A1－D1P－B1的正切值；

    (3)

    求点D到平面A1D1P的距离．

    答案：
    解析：

    (1)

    证明：∵是长方体

    ∴

    且

    (2)

    解：设

    过E作棱的垂线EF，垂足为F，连结B1F

    则EF是B1F在平面A1PD1内的射影，由三垂线定理得

    在Rt△B1EF中，…………10分

    (3)

    解：∵AD//A1D1，且

    ∴AD//平面

    ∴点D到平面的距离等于点A到平面A1D1P的距离


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

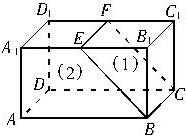    9、如图，在长方体ABCD-A1B1C1D1中，EF∥B1C1，用    平面BCFE把这个长方体分成了（1）、（2）两部分后，这两部分几何体的形状是（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图，在长方体ABCD-A1B1C1D1中，AA1=AD=a，AB=2a，E、F分别为A1B1、A1D1的中点．
    （Ⅰ）求证：AE⊥平面BCE；
    （Ⅱ）求证：DF∥平面ACE．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    定义：一点到它在一个平面内的正射影的距离叫做这一点到这个平面的距离．如图，在长方体ABCD-A1B1C1D1中，点P是侧面BCC1B1内一动点，若点P到直线C1D1的距离是点P到平面ABCD的距离的
    1
    2
    倍，则动点P的轨迹所在的曲线类型是（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2013•上海） 如图，在长方体ABCD-A′B′C′D′中，AB=2，AD=1，AA′=1．证明直线BC′平行于平面D′AC，并求直线BC′到平面D′AC的距离．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图所示，在长方体ABCD－A′B′C′D′中，截下一个棱锥C－A′DD′，求棱锥C－A′DD′的体积与剩余部分的体积之比．

    查看答案和解析>>

    同步练习册答案