
【题目】已知定义在R上的奇函数f(x)=ex﹣ae﹣x+2sinx满足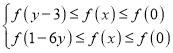 ,则z=x﹣lny的最小值是( )
,则z=x﹣lny的最小值是( )
A.﹣ln6B.﹣2C.ln6D.2
科目:高中数学 来源: 题型:
【题目】函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的部分图象如图所示,又函数![]() .
.
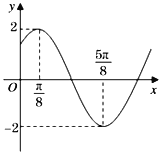
(1)求函数![]() 的单调减区间;
的单调减区间;
(2)设△ABC的内角A,B,C的对边分别为a,b,c,又![]() ,且锐角C满足
,且锐角C满足![]() ,若sinB=2sinA,求a+b的值.
,若sinB=2sinA,求a+b的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() :
:![]() ,其焦点到准线的距离为2.直线
,其焦点到准线的距离为2.直线![]() 与抛物线
与抛物线![]() 交于
交于![]() ,
,![]() 两点,过
两点,过![]() ,
,![]() 分别作抛物线
分别作抛物线![]() 的切线
的切线![]() 与
与![]() ,
,![]() 与
与![]() 交于点
交于点![]() .
.
(1)求抛物线![]() 的标准方程;
的标准方程;
(2)若![]() ,求
,求![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了释放学生压力,某校高三年级一班进行了一个投篮游戏,其间甲、乙两人轮流进行篮球定点投篮比赛(每人各投一次为一轮).在相同的条件下,每轮甲乙两人站在同一位置上,甲先投,每人投一次篮,两人有![]() 人命中,命中者得
人命中,命中者得![]() 分,未命中者得
分,未命中者得![]() 分;两人都命中或都未命中,两人均得
分;两人都命中或都未命中,两人均得![]() 分.设甲每次投篮命中的概率为
分.设甲每次投篮命中的概率为![]() ,乙每次投篮命中的概率为
,乙每次投篮命中的概率为![]() ,且各次投篮互不影响.
,且各次投篮互不影响.
(1)经过![]() 轮投篮,记甲的得分为
轮投篮,记甲的得分为![]() ,求
,求![]() 的分布列及期望;
的分布列及期望;
(2)若经过![]() 轮投篮,用
轮投篮,用![]() 表示第
表示第![]() 轮投篮后,甲的累计得分低于乙的累计得分的概率.
轮投篮后,甲的累计得分低于乙的累计得分的概率.
①求![]() ;
;
②规定![]() ,经过计算机模拟计算可得
,经过计算机模拟计算可得![]() ,请根据①中
,请根据①中![]() 值求出
值求出![]() 的值,并由此求出数列
的值,并由此求出数列![]() 的通项公式.
的通项公式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() 与椭圆
与椭圆![]() 交于不同的两点
交于不同的两点![]() ,线段
,线段![]() 的中点为
的中点为![]() ,且直线
,且直线![]() 与直线
与直线![]() 的斜率之积为
的斜率之积为![]() .若直线
.若直线![]() 与直线
与直线![]() 交于点
交于点![]() ,与直线
,与直线![]() 交于点
交于点![]() ,且
,且![]() 点为直线
点为直线![]() 上一点.
上一点.
(1)求![]() 的轨迹方程;
的轨迹方程;
(2)若![]() 为椭圆
为椭圆![]() 的上顶点,直线
的上顶点,直线![]() 与
与![]() 轴交点
轴交点![]() ,记
,记![]() 表示面积,求
表示面积,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)某中学理学社为了吸收更多新社员,在校团委的支持下,在高一学年组织了抽签赠书活动.月初报名,月末抽签,最初有30名同学参加.社团活动积极分子甲同学参加了活动.
①第一个月有18个中签名额.甲先抽签,乙和丙紧随其后抽签.求这三名同学同时中签的概率.
②理学社设置了第![]() (
(![]() )个月中签的名额为
)个月中签的名额为![]() ,并且抽中的同学退出活动,同时补充新同学,补充的同学比中签的同学少2个,如果某次抽签的同学全部中签,则活动立刻结束.求甲同学参加活动时间的期望.
,并且抽中的同学退出活动,同时补充新同学,补充的同学比中签的同学少2个,如果某次抽签的同学全部中签,则活动立刻结束.求甲同学参加活动时间的期望.
(2)某出版集团为了扩大影响,在全国组织了抽签赠书活动.报名和抽签时间与(1)中某中学理学社的报名和抽签时间相同,最初有30万人参加,甲同学在其中.每个月抽中的人退出活动,同时补充新人,补充的人数与中签的人数相同.出版集团设置了第![]() (
(![]() )个月中签的概率为
)个月中签的概率为![]() ,活动进行了
,活动进行了![]() 个月,甲同学很幸运,中签了,在此条件下,求证:甲同学参加活动时间的均值小于
个月,甲同学很幸运,中签了,在此条件下,求证:甲同学参加活动时间的均值小于![]() 个月.
个月.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com