
科目:高中数学 来源: 题型:044
如图,正方形
ABCD,有一直径为BC的半圆,BC=2cm,现有两点E、F,分别从点B、点A同时出发,点E沿线段BA以1cm/s的速度向点A运动,点F沿折线A-D-C以2 cm/s的速度向点C运动,设E离开点B的时间为t s.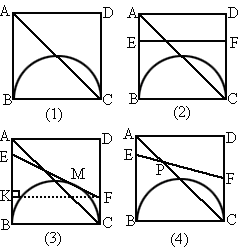
(1)
当t为何值时,线段EF与BC平行;(2)
设1<t<2,当t为何值时,EF与半圆相切?(3)
当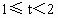 时,设EF与AC相交于点P,问点E、F运动时,点P的位置是否发生变化?若变化,请说明理由;若不变化,请给予证明,并求AP∶PC的值.
时,设EF与AC相交于点P,问点E、F运动时,点P的位置是否发生变化?若变化,请说明理由;若不变化,请给予证明,并求AP∶PC的值.查看答案和解析>>
科目:高中数学 来源: 题型:
已知![]() 是等差数列,
是等差数列,![]() 为公差且不等于
为公差且不等于![]() ,
,![]() 和
和![]() 均为实数,它的前
均为实数,它的前![]() 项和记作
项和记作![]() ,设集合
,设集合![]() ,
,![]() ,试问下列结论是否正确,如果正确,请给予证明;如果不正确,请举例说明.
,试问下列结论是否正确,如果正确,请给予证明;如果不正确,请举例说明.
(Ⅰ)若以集合![]() 中的元素作为点的坐标,则这些点都在一条直线上;
中的元素作为点的坐标,则这些点都在一条直线上;
(Ⅱ)![]() 至多有一个元素;
至多有一个元素;
(Ⅲ)当![]() 时,一定有
时,一定有![]() .
.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年江西省上饶市四校高三第二次联考数学文卷 题型:解答题
.(本题满分15分)
已知四点 ,
, ,
, ,
,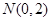 。点
。点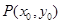 在抛物线
在抛物线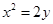 上
上
(Ⅰ) 当 时,延长
时,延长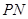 交抛物线于另一点
交抛物线于另一点 ,求
,求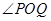 的大小;
的大小;
(Ⅱ) 当点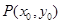
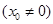 在抛物线
在抛物线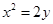 上运动时,
上运动时,
ⅰ)以 为直径作圆,求该圆截直线
为直径作圆,求该圆截直线 所得的弦长;
所得的弦长;
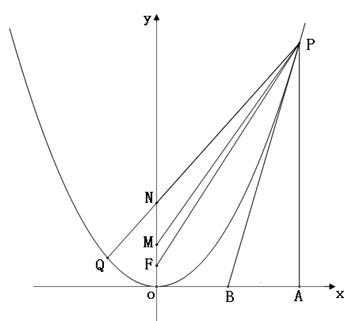
ⅱ)过点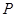 作
作 轴的垂线交
轴的垂线交 轴于点
轴于点 ,过点
,过点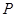 作该抛物线的切线
作该抛物线的切线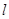 交
交 轴于点
轴于点 。问:是否总有
。问:是否总有 ?如果有,请给予证明;如果没有,请举出反例。
?如果有,请给予证明;如果没有,请举出反例。
查看答案和解析>>
科目:高中数学 来源: 题型:
已知四点![]() ,
,![]() ,
,![]() ,
,![]() 。点
。点![]() 在抛物线
在抛物线![]() 上
上
(Ⅰ) 当![]() 时,延长
时,延长![]() 交抛物线于另一点
交抛物线于另一点![]() ,求
,求![]() 的大小;
的大小;
(Ⅱ) 当点![]()
![]() 在抛物线
在抛物线![]() 上运动时,
上运动时,
ⅰ)以![]() 为直径作圆,求该圆截直线
为直径作圆,求该圆截直线![]() 所得的弦长;
所得的弦长;
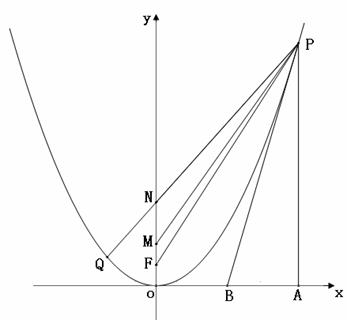
ⅱ)过点![]() 作
作![]() 轴的垂线交
轴的垂线交![]() 轴于点
轴于点![]() ,过点
,过点![]() 作该抛物线的切线
作该抛物线的切线![]() 交
交![]() 轴于点
轴于点![]() 。问:是否总有
。问:是否总有![]() ?如果有,请给予证明;如果没有,请举出反例。
?如果有,请给予证明;如果没有,请举出反例。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com