解:若a=1,则Sn=1+3+5+…+(2n-1)=n2.若a≠1,
则Sn=1+3a+5a2+…+(2n-1)an-1. ①
①式两边同乘以a,得
aSn=a+3a2+5a3+…+(2n-1)an. ②
①-②得
(1-a)Sn=1+2a+2a2+…+2an-1-(2n-1)an=1+2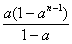 -(2n-1)an.
-(2n-1)an.
∴Sn=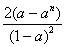 +
+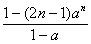 .
.
点评:这个数列可以看成一个等差数列和一个等比数列的对应项的乘积,这种数列我们称为“混合数列”,解答这类问题的常用方法是:依照等比数列前n项和公式的推导方法——错位相减法,特别要注意的是分a=1和a≠1两种情况讨论.
