
【题目】我国是全球最大的口罩生产国,在2020年3月份,我国每日口罩产量超一亿只,已基本满足国内人民的需求,但随着疫情在全球范围扩散,境外口罩需求量激增,世界卫生组织公开呼吁扩大口罩产能常见的口罩有![]() 和
和![]() (分别阻挡不少于90.0%和95.0%的0.055到0.095微米的氯化钠颗粒)两种,某口罩厂两条独立的生产线分别生产
(分别阻挡不少于90.0%和95.0%的0.055到0.095微米的氯化钠颗粒)两种,某口罩厂两条独立的生产线分别生产![]() 和
和![]() 两种口罩,为保证质量对其进行多项检测并评分(满分100分),规定总分大于或等于85分为合格,小于85分为次品,现从流水线上随机抽取这两种口罩各100个进行检测并评分,结果如下:
两种口罩,为保证质量对其进行多项检测并评分(满分100分),规定总分大于或等于85分为合格,小于85分为次品,现从流水线上随机抽取这两种口罩各100个进行检测并评分,结果如下:
总分 |
|
|
|
|
|
| 6 | 14 | 42 | 31 | 7 |
| 4 | 6 | 47 | 35 | 8 |
(1)试分别估计两种口罩的合格率;
(2)假设生产一个![]() 口罩,若质量合格,则盈利3元,若为次品则亏损1元;生产一个
口罩,若质量合格,则盈利3元,若为次品则亏损1元;生产一个![]() 口罩,若质量合格,则盈利8元,若为次品则亏损2元,在(1)的前提下,
口罩,若质量合格,则盈利8元,若为次品则亏损2元,在(1)的前提下,
①设![]() 为生产一个
为生产一个![]() 口罩和生产一个
口罩和生产一个![]() 口罩所得利润的和,求随机变量
口罩所得利润的和,求随机变量![]() 的分布列和数学期望;
的分布列和数学期望;
②求生产4个![]() 口罩所得的利润不少于8元的概率
口罩所得的利润不少于8元的概率
【答案】(1)![]() 口罩合格率为
口罩合格率为![]() ;
;![]() 合格率为
合格率为![]() (2)①分布列详见解析,数学期望为9.2;②
(2)①分布列详见解析,数学期望为9.2;②![]() .
.
【解析】
(1)根据题意,结合表中数据即可求解.
(2)①随机变量![]() 的所有可能取值为
的所有可能取值为![]() ,1,7,11,利用相互独立事件的概率乘法公式求出各随机变量的概率即可列出分布列,利用期望公式即可求解;②根据题意可知事件包括“生产4个
,1,7,11,利用相互独立事件的概率乘法公式求出各随机变量的概率即可列出分布列,利用期望公式即可求解;②根据题意可知事件包括“生产4个![]() 口罩全合格”和“生产4个
口罩全合格”和“生产4个![]() 口罩只三个合格”,由二项分布的概率求法
口罩只三个合格”,由二项分布的概率求法![]() 即可.
即可.
解(1)由题意知生产![]() 口罩合格率为
口罩合格率为![]() ,
,
生产口罩![]() 合格率为
合格率为![]() ;
;
(2)①随机变量![]() 的所有可能取值为
的所有可能取值为![]() ,1,7,11
,1,7,11
![]()
![]()
![]()
![]()
因此,![]() 的分布列如下:
的分布列如下:
|
| 1 | 7 | 11 |
|
|
|
|
|
∴![]() (元)
(元)
②设“生产4个![]() 口罩所得的利润不少于8元”事件为
口罩所得的利润不少于8元”事件为![]() ,
,
事件![]() 包括“生产4个
包括“生产4个![]() 口罩全合格”和“生产4个
口罩全合格”和“生产4个![]() 口罩只三个合格”
口罩只三个合格”
所以![]() .
.
所以生产4个![]() 口罩所得的利润不少于8元的概率为
口罩所得的利润不少于8元的概率为![]() .
.


 智慧小复习系列答案
智慧小复习系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知
中,已知![]() 、
、![]() 分别为椭圆
分别为椭圆![]() 的左、右焦点,直线
的左、右焦点,直线![]() 过点
过点![]() 且垂直于椭圆的长轴,动直线
且垂直于椭圆的长轴,动直线![]() 垂直于直线
垂直于直线![]() 于点
于点![]() ,线段
,线段![]() 的中垂线交
的中垂线交![]() 于点
于点![]() .记点
.记点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程,并说明
的方程,并说明![]() 是什么曲线;
是什么曲线;
(2)若直线![]() 与曲线
与曲线![]() 交于两点
交于两点![]() 、
、![]() ,则在圆
,则在圆![]() 上是否存在两点
上是否存在两点![]() 、
、![]() ,使得
,使得![]() ,
,![]() ?若存在,请求出
?若存在,请求出![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
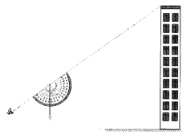
【题目】数学兴趣小组为了测量校园外一座“不可到达”建筑物的高度,采用“两次测角法”,并自制了测量工具:将一个量角器放在复印机上放大4倍复印,在中心处绑上一个铅锤,用于测量楼顶仰角(如图);推动自行车来测距(轮子滚动一周为1.753米).该小组在操场上选定A点,此时测量视线和铅锤线之间的夹角在量角器上度数为37°;推动自行车直线后退,轮子滚动了10卷达到B点,此时测量视线和铅锤线之间的夹角在量角器上度数为53°.测量者站立时的“眼高”为1.55m,根据以上数据可计算得该建筑物的高度约为___________米.(精确到0.1)
参考数据:![]() ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)求函数![]() 的图象在
的图象在![]() (
(![]() 为自然对数的底数)处的切线方程;
为自然对数的底数)处的切线方程;
(2)若对任意的![]() ,均有
,均有![]() ,则称
,则称![]() 为
为![]() 在区间
在区间![]() 上的下界函数,
上的下界函数,![]() 为
为![]() 在区间
在区间![]() 上的上界函数.
上的上界函数.
①若![]() ,求证:
,求证:![]() 为
为![]() 在
在![]() 上的上界函数;
上的上界函数;
②若![]() ,
,![]() 为
为![]() 在
在![]() 上的下界函数,求实数
上的下界函数,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于圆周率![]() ,数学发展史上出现过许多很有创意的求法,如著名的蒲丰实验和查理斯实验,受其启发,我们也可以通过设计下面的实验来估计
,数学发展史上出现过许多很有创意的求法,如著名的蒲丰实验和查理斯实验,受其启发,我们也可以通过设计下面的实验来估计![]() 的值:先请240名同学,每人随机写下两个都小于1的正实数x,y组成的实数对
的值:先请240名同学,每人随机写下两个都小于1的正实数x,y组成的实数对![]() ,再统计两数能与1构成钝角三角形三边的数对
,再统计两数能与1构成钝角三角形三边的数对![]() 的个数m;最后再根据计数m来估计π的值.假设统计结果是
的个数m;最后再根据计数m来估计π的值.假设统计结果是![]() ,那么可以估计
,那么可以估计![]() 的近似值为____________.(用分数表示)
的近似值为____________.(用分数表示)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为了解高三男生的体能达标情况,抽调了120名男生进行立定跳远测试,根据统计数据得到如下的频率分布直方图.若立定跳远成绩落在区间![]() 的左侧,则认为该学生属“体能不达标的学生,其中
的左侧,则认为该学生属“体能不达标的学生,其中![]() 分别为样本平均数和样本标准差,计算可得
分别为样本平均数和样本标准差,计算可得![]() (同一组中的数据用该组区间的中点值作代表).
(同一组中的数据用该组区间的中点值作代表).
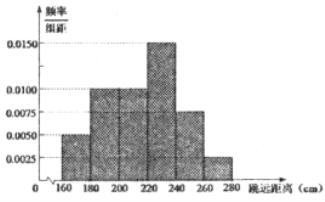
(1)若该校高三某男生的跳远距离为![]() ,试判断该男生是否属于“体能不达标”的学生?
,试判断该男生是否属于“体能不达标”的学生?
(2)该校利用分层抽样的方法从样本区间![]() 中共抽出5人,再从中选出两人进行某体能训练,求选出的两人中恰有一人跳远距离在
中共抽出5人,再从中选出两人进行某体能训练,求选出的两人中恰有一人跳远距离在![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】直角坐标系![]() 中,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,已知曲线C的极坐标方程为:
中,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,已知曲线C的极坐标方程为:![]() ,倾斜角为锐角的直线l过点
,倾斜角为锐角的直线l过点![]() 与单位圆
与单位圆![]() 相切.
相切.
(1)求曲线C的直角坐标方程和直线l的参数方程;
(2)设直线l与曲线C交于A,B两点,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com