
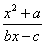 (b,c∈N)有且只有两个不动点0,2,且f(-2)<
(b,c∈N)有且只有两个不动点0,2,且f(-2)<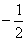 ,
,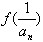 =1(Sn为数列前n项和),求数列{an}的通项公式an;
=1(Sn为数列前n项和),求数列{an}的通项公式an;解:(1)依题意有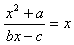 ,化简得(1-b)x2+cx+a=0,
,化简得(1-b)x2+cx+a=0,
由韦达定理,得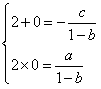 ,解得
,解得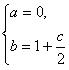 ,
,
代入表达式得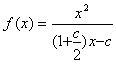 ,
,
由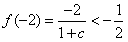 得c<3,
得c<3,
又c∈N,b∈N,
若c=0,b=1,则f(x)=x,不满足题意,
∴c=2,b=2,
故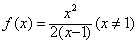 。
。
(2)由题设得 ,得:
,得: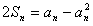 , (*)
, (*)
且an≠1,用n-1代n得: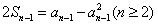 ,(**)
,(**)
(*)与(**)两式相减得: ,
,
即 ,
,
∴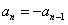 或
或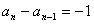 ,
,
把n=1代入(*)得: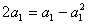 ,
,
解得a1=0(舍去)或a1=-1,
若 ,得a2=1,这与an≠1矛盾,
,得a2=1,这与an≠1矛盾,
∴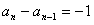 ,即{an}是以-1为首项,-1为公差的等差数列,
,即{an}是以-1为首项,-1为公差的等差数列,
∴an=-n。
(3)采用反证法,假设an≥3(n≥2),则由(1)知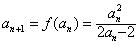 ,
,
∴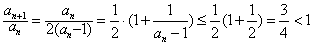 ,
,
即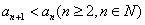 ,有
,有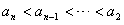 ,
,
而当n=2时,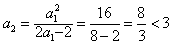 ,
,
∴an<3,这与假设矛盾,故假设不成立,
∴an<3。


科目:高中数学 来源: 题型:
(08年黄冈中学一模理) (本小题满分14分)对于函数f(x),若存在![]() ,使
,使![]() 成立,则称x0为f(x)的不动点. 如果函数
成立,则称x0为f(x)的不动点. 如果函数![]() 有且仅有两个不动点0,2,且
有且仅有两个不动点0,2,且![]()
(1)试求函数f(x)的单调区间;
(2)已知各项不为零且不为1的数列{an}满足![]() ,求证:
,求证:![]() ;
;
(3)设![]() ,
,![]() 为数列{bn}的前n项和,求证:
为数列{bn}的前n项和,求证:![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
对于函数f(x),若存在x0∈R,使f(x0)=x0成立,则称x0为f(x)的不动点![]() 已知函数f(x)=ax2+(b+1)x+(b–1)(a≠0)
已知函数f(x)=ax2+(b+1)x+(b–1)(a≠0)
(1)若a=1,b=–2时,求f(x)的不动点;
(2)若对任意实数b,函数f(x)恒有两个相异的不动点,求a的取值范围;
(3)在(2)的条件下,若y=f(x)图像上A、B两点的横坐标是函数f(x)的不动点,且A、B关于直线y=kx+![]() 对称,求b的最小值.
对称,求b的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
对于函数f(x),若存在x0∈R,使f(x0)=x0成立,则称x0为f(x)的不动点.如果函数
f(x)=ax2+bx+1(a>0)有两个相异的不动点x1,x2.
⑴若x1<1<x2,且f(x)的图象关于直线x=m对称,求证:![]() <m<1;
<m<1;
⑵若|x1|<2且|x1-x2|=2,求b的取值范围.
查看答案和解析>>
科目:高中数学 来源:2014届湖南师大附中高三第二次月考理科数学试卷(解析版) 题型:填空题
对于函数f(x),若在其定义域内存在两个实数a,b(a<b),使当x∈[a,b]时,f(x)的值域也是[a,b],则称函数f(x)为“布林函数”,区间[a,b]称为函数f(x)的“等域区间”.
(1)布林函数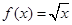 的等域区间是 .
的等域区间是 .
(2)若函数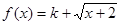 是布林函数,则实数k的取值范围是
.
是布林函数,则实数k的取值范围是
.
查看答案和解析>>
科目:高中数学 来源:2014届湖南省华容县高一第一学期期末考试数学试卷 题型:解答题
(本小题满分6分)对于函数f(x),若存在x0ÎR,使f(x0)=x0成立,则称点(x0,x0)为函数的不动点,已知函数f(x)=ax2+bx-b有不动点(1,1)和(-3,-3),求a、b的值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com