
【题目】已知函数![]() (其中e为自然对数的底).
(其中e为自然对数的底).
(1)若![]() 在
在![]() 上单调递增,求实数a的取值范围;
上单调递增,求实数a的取值范围;
(2)若![]() ,证明:
,证明:![]() 存在唯一的极小值点
存在唯一的极小值点![]() ,且
,且![]() .
.
【答案】(1)![]() ;(2)证明见解析
;(2)证明见解析
【解析】
(1)求导得![]() ,则
,则![]() 在
在![]() 时恒成立,不等式可转化为
时恒成立,不等式可转化为![]() ,求出
,求出![]() 的最小值,令
的最小值,令![]() 即可;
即可;
(2)![]() 时,
时,![]() ,求出导函数,可知
,求出导函数,可知![]() 单调递增,令
单调递增,令![]() ,易证
,易证![]() ,从而可证明
,从而可证明![]() 存在唯一的极小值点
存在唯一的极小值点![]() ,再结合
,再结合![]() ,可得到
,可得到![]() 和
和![]() ,从而可得到
,从而可得到![]() 的表达式,结合
的表达式,结合![]() ,求出
,求出![]() 的取值范围即可.
的取值范围即可.
(1)由题意,![]() ,则
,则![]() 在
在![]() 时恒成立,即
时恒成立,即![]() 在
在![]() 时恒成立,
时恒成立,
令![]() ,则
,则![]() ,显然
,显然![]() 在
在![]() 上单调递增,则
上单调递增,则![]() ,所以只需
,所以只需![]() ,即满足
,即满足![]() 在
在![]() 时恒成立,
时恒成立,
故实数a的取值范围是![]() .
.
(2)![]() ,则
,则![]() ,其定义域为
,其定义域为![]() ,
,
求导得![]() ,显然
,显然![]() 是
是![]() 上的增函数,
上的增函数,
![]() ,因为
,因为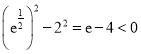 ,所以
,所以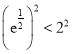 ,即
,即![]() ,
,
![]() ,因为
,因为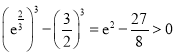 ,所以
,所以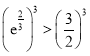 ,即
,即![]() ,
,
令![]() ,则
,则![]() 在
在![]() 上有唯一零点
上有唯一零点![]() ,且
,且![]() ,
,
故![]() 时,
时,![]() 单调递减,
单调递减,![]() 时,
时,![]() 单调递增,所以
单调递增,所以![]() 存在唯一的极小值点
存在唯一的极小值点![]() .
.
因为![]() ,所以
,所以![]() ,两边取对数得
,两边取对数得![]() ,即
,即![]() ,
,
故![]() ,
,![]() ,
,
构造函数![]() ,
,![]() ,
,
显然![]() 在
在![]() 上单调递减,所以
上单调递减,所以![]() ,
,
又![]() ,
,![]() ,故
,故![]() ,即
,即![]() .
.
所以![]() 存在唯一的极小值点
存在唯一的极小值点![]() ,且
,且![]() .
.


 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() 的图象的一个对称中心为
的图象的一个对称中心为![]() ,则下列说法正确的是( )
,则下列说法正确的是( )
A.直线![]() 是函数
是函数![]() 的图象的一条对称轴
的图象的一条对称轴
B.函数![]() 在
在![]() 上单调递减
上单调递减
C.函数![]() 的图象向右平移
的图象向右平移![]() 个单位可得到
个单位可得到![]() 的图象
的图象
D.函数![]() 在
在![]() 上的最小值为
上的最小值为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的一个焦点为
的一个焦点为![]() ,离心率为
,离心率为![]() .
.
(1)求![]() 的标准方程;
的标准方程;
(2)若动点![]() 为
为![]() 外一点,且
外一点,且![]() 到
到![]() 的两条切线相互垂直,求
的两条切线相互垂直,求![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(3)设![]() 的另一个焦点为
的另一个焦点为![]() ,自直线
,自直线![]() :
:![]() 上任意一点
上任意一点![]() 引(2)所求轨迹
引(2)所求轨迹![]() 的一条切线,切点为
的一条切线,切点为![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】法国有个名人叫做布莱尔·帕斯卡,他认识两个赌徒,这两个赌徒向他提出一个问题,他们说,他们下赌金之后,约定谁先赢满5局,谁就获得全部赌金700法郎,赌了半天,甲赢了4局,乙赢了3局,时间很晚了,他们都不想再赌下去了.假设每局两赌徒输赢的概率各占![]() ,每局输赢相互独立,那么这700法郎如何分配比较合理( )
,每局输赢相互独立,那么这700法郎如何分配比较合理( )
A.甲400法郎,乙300法郎B.甲500法郎,乙200法郎
C.甲525法郎,乙175法郎D.甲350法郎,乙350法郎
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() ,
,![]() ,
,![]() 是三个不同平面,
是三个不同平面,![]() ,
,![]() 是两条不同直线,有下列三个条件:(1)
是两条不同直线,有下列三个条件:(1)![]() ,
,![]() ;(2)
;(2)![]() ,
,![]() ;(3)
;(3)![]() ,
,![]() .如果命题“
.如果命题“![]() ,
,![]() ,且__________,则
,且__________,则![]() ”为真命题,则可以在横线处填入的条件是__________(把所有正确的序号填上).
”为真命题,则可以在横线处填入的条件是__________(把所有正确的序号填上).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
某营养师要为某个儿童预定午餐和晚餐.已知一个单位的午餐含12个单位的碳水化合物,6个单位的蛋白质和6个单位的维生素![]() ;一个单位的晚餐含8个单位的碳水化合物,6个单位的蛋白质和10个单位的维生素
;一个单位的晚餐含8个单位的碳水化合物,6个单位的蛋白质和10个单位的维生素![]() .另外,该儿童这两餐需要的营养中至少含64个单位的碳水化合物,42个单位的蛋白质和54个单位的维生素
.另外,该儿童这两餐需要的营养中至少含64个单位的碳水化合物,42个单位的蛋白质和54个单位的维生素![]() .如果一个单位的午餐、晚餐的费用分别是2.5元和4元,那么要满足上述的营养要求,并且花费最少,应当为该儿童分别预订多少个单位的午餐和晚餐?
.如果一个单位的午餐、晚餐的费用分别是2.5元和4元,那么要满足上述的营养要求,并且花费最少,应当为该儿童分别预订多少个单位的午餐和晚餐?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com