
ЎҫМвДҝЎҝДіЦЦІъЖ·өДЦКБҝТФЖдЦКБҝЦёұкЦөәвБҝЈ¬ІўТАҫЭЦКБҝЦёұкЦө»®·ЦөИј¶ИзұнЈә
ЦКБҝЦёұкЦөm | 25ЎЬmЈј35 | 15ЎЬmЈј25»т35ЎЬmЈј45 | 0ЈјmЈј15»т45ЎЬmЈј65 |
өИј¶ | Т»өИЖ· | ¶юөИЖ· | ИэөИЖ· |
ДіЖуТөҙУЙъІъөДХвЦЦІъЖ·ЦРійИЎ100јюІъЖ·ЧчОӘСщұҫЈ¬јмІвЖдЦКБҝЦёұкЦөЈ¬өГөҪПВНјөДВК·ЦІјЦұ·ҪНјЈ®ЈЁН¬Т»ЧйКэҫЭУГёГЗшјдөДЦРөгЦөЧчҙъұнЈ©
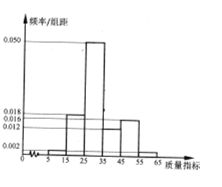
ЈЁ1Ј©ёГЖуТөОӘМбёЯІъЖ·ЦКБҝЈ¬ҝӘХ№БЛЦКБҝМбЙэФВЎұ»о¶ҜЈ¬»о¶ҜәуФЩійСщјмІвЈ¬ІъЖ·ИэөИЖ·КэYҪьЛЖВъЧгYЎ«HЈЁ10Ј¬15Ј¬100Ј©Ј¬ЗлІвЛгЎ°ЦКБҝМбЙэФВЎұ»о¶ҜәуХвЦЦІъЖ·өДЎ°¶юөИЖ·ВКЎ°ЈЁТ»Ўў¶юөИЖ·ЖдХјИ«ІҝІъЖ·°Щ·ЦұИЈ©ҪП»о¶ҜЗ°МбёЯ¶аЙЩёц°Щ·ЦөгЈҝ
ЈЁ2Ј©ИфЖуТөГҝјюТ»өИЖ·КЫјЫ180ФӘЈ¬Гҝјю¶юөИЖ·КЫјЫ150ФӘЈ¬ГҝјюИэөИЖ·КЫјЫ120ФӘЈ¬ТФСщұҫЦРөДЖөВКҙъМжПаУҰёЕВКЈ¬ПЦУРТ»ГыБӘҝНЛж»ъ№әВтБҪјюІъЖ·Ј¬ЙиЖдЦ§ё¶өД·СУГОӘXЈЁөҘО»ЈәФӘЈ©Ј¬ЗуXөД·ЦІјБРј°КэС§ЖЪНыЈ®
Ўҫҙр°ёЎҝЈЁ1Ј©5ёц°Щ·ЦөгЈ®ЈЁ2Ј©јыҪвОцЈ¬![]() Ј®
Ј®
ЎҫҪвОцЎҝ
ЈЁ1Ј©ёщҫЭійСщөчІйКэҫЭЈ¬ЗуөГСщұҫЦРТ»өИЖ·әН¶юөИЖ·өДјюКэЈ¬өГөҪФЪСщұҫЦРЛщХјұИАэЈ¬ФЩёщҫЭ»о¶ҜәуІъЖ·ИэөИЖ·КэYҪьЛЖВъЧгYЎ«HЈЁ10Ј¬15Ј¬100Ј©өГөҪТ»Ўў¶юөИЖ·өДәПёсВКЈ¬БҪёцұИАэұИҪПјҙҝЙ.
ЈЁ2Ј©ёщҫЭСщЖ·№АјЖЧЬМеЈ¬ёГЖуТөЛж»ъійИЎТ»јюІъЖ·ОӘТ»өИЖ·өДёЕВКОӘ![]() Ј¬¶юөИЖ·өДёЕВКОӘ
Ј¬¶юөИЖ·өДёЕВКОӘ![]() Ј¬ИэөИЖ·өДёЕВКОӘ
Ј¬ИэөИЖ·өДёЕВКОӘ![]() Ј¬ФЩГчИ·Лж»ъұдБҝXөДЛщУРҝЙДЬИЎЦөОӘ240Ј¬270Ј¬300Ј¬330Ј¬360Ј¬·ЦұрЗуөГПаУҰёЕВКЈ¬Рҙіц·ЦІјБРФЩЗуЖЪНы.
Ј¬ФЩГчИ·Лж»ъұдБҝXөДЛщУРҝЙДЬИЎЦөОӘ240Ј¬270Ј¬300Ј¬330Ј¬360Ј¬·ЦұрЗуөГПаУҰёЕВКЈ¬Рҙіц·ЦІјБРФЩЗуЖЪНы.
ЈЁ1Ј©ёщҫЭійСщөчІйКэҫЭЦӘЈ¬СщұҫЦРТ»өИЖ·әН¶юөИЖ·№ІУРЈәЈЁ0.5+0.18+0.12Ј©ЎБ100ЈҪ80ЈЁјюЈ©
ФЪСщұҫЦРЛщХјұИАэОӘ80%Ј¬
»о¶ҜәуІъЖ·ИэөИЖ·КэYҪьЛЖВъЧгYЎ«HЈЁ10Ј¬15Ј¬100Ј©Ј¬
ЛщТФ100јюІъЖ·ЦРИэөИЖ·ОӘ15јюЈ¬Т»Ўў¶юөИЖ·КэОӘ100©Ғ15ЈҪ85ЈЁјюЈ©әПёсВКОӘ85%Ј¬
ЛщТФТ»Ўў¶юөИЖ·ВКФцјУБЛ5ёц°Щ·ЦөгЈ®
ЈЁ2Ј©УЙСщЖ·№АјЖЧЬМеЦӘЈ¬ёГЖуТөЛж»ъійИЎТ»јюІъЖ·ОӘТ»өИЖ·өДёЕВКОӘ![]() Ј¬¶юөИЖ·өДёЕВКОӘ
Ј¬¶юөИЖ·өДёЕВКОӘ![]() Ј¬ИэөИЖ·өДёЕВКОӘ
Ј¬ИэөИЖ·өДёЕВКОӘ![]() Ј¬
Ј¬
Лж»ъұдБҝXөДЛщУРҝЙДЬИЎЦөОӘ240Ј¬270Ј¬300Ј¬330Ј¬360Ј®
![]() Ј¬
Ј¬
![]() Ј¬
Ј¬
![]() Ј¬
Ј¬
![]() Ј®
Ј®
![]() Ј¬
Ј¬
ЛщТФXөД·ЦІјБРОӘЈә
X | 240 | 270 | 300 | 330 | 360 |
PЈЁXЈ© |
|
|
|
|
|
XөДКэС§ЖЪНы![]() Ј®
Ј®


 МмМмПтЙПТ»ұҫәГҫнПөБРҙр°ё
МмМмПтЙПТ»ұҫәГҫнПөБРҙр°ё РЎС§Йъ10·ЦЦУУҰУГМвПөБРҙр°ё
РЎС§Йъ10·ЦЦУУҰУГМвПөБРҙр°ё
| Дкј¶ | ёЯЦРҝОіМ | Дкј¶ | іхЦРҝОіМ |
| ёЯТ» | ёЯТ»Гв·СҝОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СҝОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СҝОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СҝОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СҝОіМНЖјцЈЎ | іхИэ | іхИэГв·СҝОіМНЖјцЈЎ |
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝ¶ФУЪјҜәП![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬¶ЁТе
Ј¬¶ЁТе![]() .
.
јҜәП![]() ЦРөДФӘЛШёцКэјЗОӘ
ЦРөДФӘЛШёцКэјЗОӘ![]() Ј¬өұ
Ј¬өұ![]() Ј¬іЖјҜәП
Ј¬іЖјҜәП![]() ҫЯУРРФЦК
ҫЯУРРФЦК![]() .
.
ЈЁ1Ј©ТСЦӘјҜәП![]() Ј¬
Ј¬![]() Ј¬Рҙіц
Ј¬Рҙіц![]() Ј¬
Ј¬![]() өДЦөЈ¬ІўЕР¶ПјҜәП
өДЦөЈ¬ІўЕР¶ПјҜәП![]() КЗ·сҫЯУРРФЦК
КЗ·сҫЯУРРФЦК![]() Ј»
Ј»
ЈЁ2Ј©ЙијҜәП![]() ҫЯУРРФЦК
ҫЯУРРФЦК![]() Ј¬ЕР¶ПјҜәП
Ј¬ЕР¶ПјҜәП![]() ЦРөДИэёцФӘЛШКЗ·сДЬЧйіЙөИІоКэБРЈ¬ЗлЛөГчАнУЙЈ»
ЦРөДИэёцФӘЛШКЗ·сДЬЧйіЙөИІоКэБРЈ¬ЗлЛөГчАнУЙЈ»
ЈЁ3Ј©ИфКэБР![]() КЗТФ
КЗТФ![]() ОӘКЧПоЈ¬2ОӘ№«ұИөДөИұИКэБР. КэБР
ОӘКЧПоЈ¬2ОӘ№«ұИөДөИұИКэБР. КэБР![]() ЦРөДЗ°100ПоЈә
ЦРөДЗ°100ПоЈә![]() ЧйіЙөДјҜәП
ЧйіЙөДјҜәП![]() јЗЧч
јЗЧч![]() Ј¬Ҫ«јҜәП
Ј¬Ҫ«јҜәП![]() ЦРөДЛщУРФӘЛШ
ЦРөДЛщУРФӘЛШ![]() ҙУРЎөҪҙуЕЕРтЈ¬јҙ
ҙУРЎөҪҙуЕЕРтЈ¬јҙ![]() ВъЧг
ВъЧг![]() Ј¬Зу
Ј¬Зу![]() .
.
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝСЎРЮ4-4ЈәЧшұкПөУлІОКэ·ҪіМ
ФЪЖҪГжЦұҪЗЧшұкПөЦРЈ¬ТФЧшұкФӯөгОӘј«өгЈ¬ТФ![]() ЦбХэ°лЦбОӘј«ЦбЈ¬ҪЁБўј«ЧшұкПөЈ¬өг
ЦбХэ°лЦбОӘј«ЦбЈ¬ҪЁБўј«ЧшұкПөЈ¬өг![]() өДј«ЧшұкОӘ
өДј«ЧшұкОӘ![]() Ј¬ЦұПЯ
Ј¬ЦұПЯ![]() өДј«Чшұк·ҪіМОӘ
өДј«Чшұк·ҪіМОӘ![]() Ј¬ЗТ
Ј¬ЗТ![]() №эөг
№эөг![]() Ј¬ЗъПЯ
Ј¬ЗъПЯ![]() өДІОКэ·ҪіМОӘ
өДІОКэ·ҪіМОӘ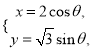 (
(![]() ОӘІОКэ).
ОӘІОКэ).
(ўс)ЗуЗъПЯ![]() ЙПөДөгөҪЦұПЯ
ЙПөДөгөҪЦұПЯ![]() өДҫаАлөДЧоҙуЦөЈ»
өДҫаАлөДЧоҙуЦөЈ»
(ўт)№эөг![]() УлЦұПЯ
УлЦұПЯ![]() ЖҪРРөДЦұПЯ
ЖҪРРөДЦұПЯ![]() УлЗъПЯ
УлЗъПЯ ![]() Ҫ»УЪ
Ҫ»УЪ![]() БҪөгЈ¬Зу
БҪөгЈ¬Зу![]() өДЦө.
өДЦө.
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЈ¬ФЪЖҪРРЛДұЯРО![]() ЦРЈ¬
ЦРЈ¬![]() Ј¬
Ј¬![]() Ј¬ПЦСШ¶ФҪЗПЯ
Ј¬ПЦСШ¶ФҪЗПЯ![]() Ҫ«
Ҫ«![]() ХЫЖрЈ¬К№өгAөҪҙпөгPЈ¬өгMЈ¬N·ЦұрФЪЦұПЯ
ХЫЖрЈ¬К№өгAөҪҙпөгPЈ¬өгMЈ¬N·ЦұрФЪЦұПЯ![]() Ј¬
Ј¬![]() ЙПЈ¬ЗТAЈ¬BЈ¬MЈ¬NЛДөг№ІГж.
ЙПЈ¬ЗТAЈ¬BЈ¬MЈ¬NЛДөг№ІГж.
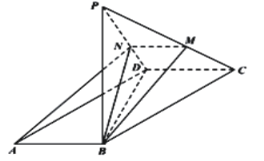
ЈЁ1Ј©ЗуЦӨЈә![]() Ј»
Ј»
ЈЁ2Ј©ИфЖҪГж![]() ЖҪГж
ЖҪГж![]() Ј¬¶юГжҪЗ
Ј¬¶юГжҪЗ![]() ЖҪГжҪЗҙуРЎОӘ
ЖҪГжҪЗҙуРЎОӘ![]() Ј¬ЗуЦұПЯ
Ј¬ЗуЦұПЯ![]() УлЖҪГж
УлЖҪГж![]() ЛщіЙҪЗөДХэПТЦө.
ЛщіЙҪЗөДХэПТЦө.
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТСЦӘКэБР{an}ВъЧг![]() Ј®
Ј®
ЈЁ1Ј©Зуa1Ј¬a2Ј¬a3өДЦөЈ»
ЈЁ2Ј©¶ФИОТвХэХыКэnЈ¬anРЎКэөгәуөЪТ»О»КэЧЦКЗ¶аЙЩЈҝЗлЛөГчАнУЙЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзіЗДі№Ы№вЗшөДЖҪГжКҫТвНјИзНјЛщКҫЈ¬ЖдЦРҫШРО![]() өДіӨ
өДіӨ![]() З§ГЧЈ¬ҝн
З§ГЧЈ¬ҝн![]() З§ГЧЈ¬°лФІөДФІРД
З§ГЧЈ¬°лФІөДФІРД![]() ОӘ
ОӘ![]() ЦРөг.ОӘБЛұгУЪУОҝН№Ы№вРЭПРЈ¬ФЪ№Ы№вЗшЖМЙиТ»МхУЙФІ»Ў
ЦРөг.ОӘБЛұгУЪУОҝН№Ы№вРЭПРЈ¬ФЪ№Ы№вЗшЖМЙиТ»МхУЙФІ»Ў![]() ЎўПЯ¶О
ЎўПЯ¶О![]() Ўў
Ўў![]() ЧйіЙөД№Ы№вөАВ·.ЖдЦРПЯ¶О
ЧйіЙөД№Ы№вөАВ·.ЖдЦРПЯ¶О![]() ҫӯ№эФІРД
ҫӯ№эФІРД![]() Ј¬ЗТөг
Ј¬ЗТөг![]() ФЪПЯ¶О
ФЪПЯ¶О![]() ЙПЈЁІ»ә¬ПЯ¶О¶Лөг
ЙПЈЁІ»ә¬ПЯ¶О¶Лөг![]() Ўў
Ўў![]() Ј©.ТСЦӘөАВ·
Ј©.ТСЦӘөАВ·![]() Ўў
Ўў![]() өДФмјЫОӘ
өДФмјЫОӘ![]() ФӘГҝЗ§ГЧЈ¬өАВ·
ФӘГҝЗ§ГЧЈ¬өАВ·![]() ФмјЫОӘ
ФмјЫОӘ![]() ФӘГҝЗ§ГЧЈ¬Йи
ФӘГҝЗ§ГЧЈ¬Йи![]() Ј¬№Ы№вөАВ·өДЧЬФмјЫОӘ
Ј¬№Ы№вөАВ·өДЧЬФмјЫОӘ![]() .
.
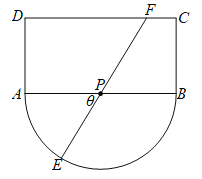
ЈЁ1Ј©КФЗу![]() Ул
Ул![]() өДәҜКэ№ШПөКҪЈә
өДәҜКэ№ШПөКҪЈә![]() Ј»
Ј»
ЈЁ2Ј©өұ![]() ОӘәОЦөКұЈ¬№Ы№вөАВ·өДЧЬФмјЫ
ОӘәОЦөКұЈ¬№Ы№вөАВ·өДЧЬФмјЫ![]() ЧоРЎ.
ЧоРЎ.
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝЦР№ъ№ЕҙъИејТТӘЗуС§ЙъХЖОХБщЦЦ»щұҫІЕТХЈәАсЎўАЦЎўЙдЎўУщЎўКйЎўКэЈ¬јтіЖЎ°БщТХЎұ,ДіёЯЦРѧУОӘәлСпЎ°БщТХЎұөДҙ«НіОД»ҜЈ¬·ЦұрҪшРРБЛЦчМвОӘЎ°АсЎўАЦЎўЙдЎўУщЎўКйЎўКэЎұБщіЎҙ«НіОД»ҜЦӘК¶ҫәИьЈ¬ПЦУРјЧЎўТТЎўұыИэО»СЎКЦҪшИлБЛЗ°ИэГыөДЧоәуҪЗЦр,№ж¶ЁЈәГҝіЎЦӘК¶ҫәИьЗ°ИэГыөДөГ·Ц¶ј·ЦұрОӘ![]()
![]() ЗТ
ЗТ![]() Ј»СЎКЦЧоәуөГ·ЦОӘёчіЎөГ·ЦЦ®әНЈ¬ФЪБщіЎұИИьәуЈ¬ТСЦӘјЧЧоәуөГ·ЦОӘ
Ј»СЎКЦЧоәуөГ·ЦОӘёчіЎөГ·ЦЦ®әНЈ¬ФЪБщіЎұИИьәуЈ¬ТСЦӘјЧЧоәуөГ·ЦОӘ![]() ·ЦЈ¬ТТәНұыЧоәуөГ·Ц¶јКЗ
·ЦЈ¬ТТәНұыЧоәуөГ·Ц¶јКЗ![]() ·ЦЈ¬ЗТТТФЪЖдЦРТ»іЎұИИьЦР»сөГөЪТ»ГыЈ¬ПВБРЛө·ЁХэИ·өДКЗ( )
·ЦЈ¬ЗТТТФЪЖдЦРТ»іЎұИИьЦР»сөГөЪТ»ГыЈ¬ПВБРЛө·ЁХэИ·өДКЗ( )
A. ТТУРЛДіЎұИИь»сөГөЪИэГы
B. ГҝіЎұИИьөЪТ»ГыөГ·Ц![]() ОӘ
ОӘ![]()
C. јЧҝЙДЬУРТ»іЎұИИь»сөГөЪ¶юГы
D. ұыҝЙДЬУРТ»іЎұИИь»сөГөЪТ»Гы
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝЙиЦұПЯ![]() УлЦұПЯ
УлЦұПЯ![]() ·ЦұрУлНЦФІ
·ЦұрУлНЦФІ![]()
![]() Ҫ»УЪөг
Ҫ»УЪөг![]() Ј¬ЗТЛДұЯРО
Ј¬ЗТЛДұЯРО![]() өДГж»эОӘ
өДГж»эОӘ![]() .
.
ЈЁ1Ј©ЗуНЦФІ![]() өД·ҪіМЈ»
өД·ҪіМЈ»
ЈЁ2Ј©Йи№эөг![]() өД¶ҜЦұПЯ
өД¶ҜЦұПЯ![]() УлНЦФІ
УлНЦФІ![]() ПаҪ»УЪ
ПаҪ»УЪ![]() Ј¬
Ј¬![]() БҪөгЈ¬КЗ·сҙжФЪҫӯ№эФӯөгЈ¬ЗТТФ
БҪөгЈ¬КЗ·сҙжФЪҫӯ№эФӯөгЈ¬ЗТТФ![]() ОӘЦұҫ¶өДФІЈҝИфУРЈ¬ЗлЗуіцФІөД·ҪіМЈ¬ИфГ»УРЈ¬ЗлЛөГчАнУЙ.
ОӘЦұҫ¶өДФІЈҝИфУРЈ¬ЗлЗуіцФІөД·ҪіМЈ¬ИфГ»УРЈ¬ЗлЛөГчАнУЙ.
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТСЦӘЕЧОпПЯCЈәx2=2pyҫӯ№эөгЈЁ2Ј¬1Ј©Ј®
ЈЁўсЈ©ЗуЕЧОпПЯCөД·ҪіМј°ЖдЧјПЯ·ҪіМЈ»
ЈЁўтЈ©ЙиOОӘФӯөгЈ¬№эЕЧОпПЯCөДҪ№өгЧчРұВКІ»ОӘ0өДЦұПЯlҪ»ЕЧОпПЯCУЪБҪөгMЈ¬NЈ¬ЦұПЯy=1·ЦұрҪ»ЦұПЯOMЈ¬ONУЪөгAәНөгB.ЗуЦӨЈәТФABОӘЦұҫ¶өДФІҫӯ№эyЦбЙПөДБҪёц¶ЁөгЈ®
Ійҝҙҙр°ёәНҪвОц>>
°Щ¶ИЦВРЕ - Б·П°ІбБРұн - КФМвБРұн
әюұұКЎ»ҘБӘНшОҘ·ЁәНІ»БјРЕПўҫЩұЁЖҪМЁ | НшЙПУРәҰРЕПўҫЩұЁЧЁЗш | өзРЕХ©ЖӯҫЩұЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРәҰРЕПўҫЩұЁЧЁЗш | ЙжЖуЗЦИЁҫЩұЁЧЁЗш
ОҘ·ЁәНІ»БјРЕПўҫЩұЁөз»°Јә027-86699610 ҫЩұЁУКПдЈә58377363@163.com