
【题目】为建设美丽乡村,政府欲将一块长12百米,宽5百米的矩形空地ABCD建成生态休闲园,园区内有一景观湖EFG(图中阴影部分),以AB所在直线为x轴,AB的垂直平分线为y轴,建立平面直角坐标系xOy(如图所示).景观湖的边界线符合函数y=x+ ![]() (x>0)模型,园区服务中心P在x轴正半轴上,PO=
(x>0)模型,园区服务中心P在x轴正半轴上,PO= ![]() 百米.
百米. 
(1)若在点O和景观湖边界曲线上一点M之间修建一条休闲长廊OM,求OM的最短长度;
(2)若在线段DE上设置一园区出口Q,试确定Q的位置,使通道PQ最短.
【答案】
(1)解:设M(x,x+ ![]() ),则|OM|2=x2+(x+
),则|OM|2=x2+(x+ ![]() )2=2x2+
)2=2x2+ ![]() +2≥2
+2≥2 ![]() +2,
+2,
当且仅当2x2= ![]() 即x2=
即x2= ![]() 时取等号,
时取等号,
∴|OM|的最短距离为 ![]()
(2)解:过P作函数y=x+ ![]() 的切线l,设切线l的方程为y=k(x﹣
的切线l,设切线l的方程为y=k(x﹣ ![]() )(k<0),
)(k<0),
联立方程组 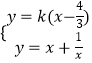 ,得(1﹣k)x2+
,得(1﹣k)x2+ ![]() x+1=0,
x+1=0,
令△= ![]() k2﹣4(1﹣k)=0得k=﹣3或k=
k2﹣4(1﹣k)=0得k=﹣3或k= ![]() (舍),
(舍),
∴直线l的方程为y=﹣3(x﹣ ![]() ),
),
令y=5得x=﹣ ![]() ,
,
∴DQ=6﹣ ![]() =
= ![]() .
.
∴当|DQ|= ![]() 时,通道PQ最短
时,通道PQ最短
【解析】(1)设M(x,x+ ![]() ),利用距离公式得出|OM|2关于x的函数,利用基本不等式求出最小值即可;(2)当直线PQ与湖边界相切时,通道最短,设出切线方程,与边界函数联立,令△=0即可得出切线方程,从而确定Q点的位置.
),利用距离公式得出|OM|2关于x的函数,利用基本不等式求出最小值即可;(2)当直线PQ与湖边界相切时,通道最短,设出切线方程,与边界函数联立,令△=0即可得出切线方程,从而确定Q点的位置.


科目:高中数学 来源: 题型:
【题目】一个多面体的直观图、正视图、侧视图、俯视图如图,M,N分别为A1B,B1C1的中点.
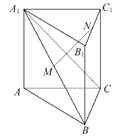
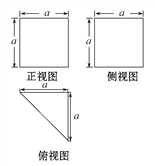
下列结论中正确的个数有 ( )
①直线MN与A1C相交.
②MN⊥BC.
③MN∥平面ACC1A1.
④三棱锥N-A1BC的体积为![]() =
=![]() a3.
a3.
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是一座桥的截面图,桥的路面由三段曲线构成,曲线AB和曲线DE分别是顶点在路面A、E的抛物线的一部分,曲线BCD是圆弧,已知它们在接点B、D处的切线相同,若桥的最高点C到水平面的距离H=6米,圆弧的弓高h=1米,圆弧所对的弦长BD=10米. 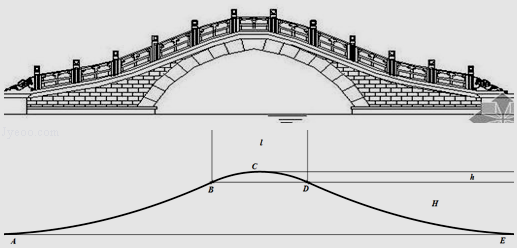
(1)求弧 ![]() 所在圆的半径;
所在圆的半径;
(2)求桥底AE的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆M:![]() 与
与![]() 轴相切.
轴相切.
(1)求![]() 的值;
的值;
(2)求圆M在![]() 轴上截得的弦长;
轴上截得的弦长;
(3)若点![]() 是直线
是直线![]() 上的动点,过点
上的动点,过点![]() 作直线
作直线![]() 与圆M相切,
与圆M相切,![]() 为切点,求四边形
为切点,求四边形![]() 面积的最小值.
面积的最小值.
【答案】(1) ![]() (2)
(2) ![]() (3)
(3) ![]()
【解析】试题分析:(1)先将圆的一般方程化成标准方程,利用直线和圆相切进行求解;(2) 令![]() ,得到关于
,得到关于![]() 的一元二次方程进行求解;(3)将四边形的面积的最小值问题转化为点到直线的的距离进行求解.
的一元二次方程进行求解;(3)将四边形的面积的最小值问题转化为点到直线的的距离进行求解.
试题解析:(1) ![]() ∵圆M:
∵圆M:![]() 与
与![]() 轴相切
轴相切
∴![]() ∴
∴![]()
(2) 令![]() ,则
,则![]() ∴
∴![]()
∴![]()
(3) ![]()
∵![]() 的最小值等于点
的最小值等于点![]() 到直线
到直线![]() 的距离,
的距离,
∴![]() ∴
∴![]()
∴四边形![]() 面积的最小值为
面积的最小值为![]() .
.
【题型】解答题
【结束】
20
【题目】在平面直角坐标系![]() 中,圆
中,圆![]() 的方程为
的方程为![]() ,且圆
,且圆![]() 与
与![]() 轴交于
轴交于![]() ,
, ![]() 两点,设直线
两点,设直线![]() 的方程为
的方程为![]() .
.
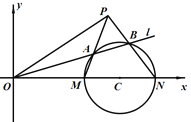
(1)当直线![]() 与圆
与圆![]() 相切时,求直线
相切时,求直线![]() 的方程;
的方程;
(2)已知直线![]() 与圆
与圆![]() 相交于
相交于![]() ,
, ![]() 两点.
两点.
(ⅰ)若![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(ⅱ)直线![]() 与直线
与直线![]() 相交于点
相交于点![]() ,直线
,直线![]() ,直线
,直线![]() ,直线
,直线![]() 的斜率分别为
的斜率分别为![]() ,
, ![]() ,
, ![]() ,
,
是否存在常数![]() ,使得
,使得![]() 恒成立?若存在,求出
恒成立?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量m ![]() (sin
(sin ![]() ,1),
,1), ![]() =(1,
=(1, ![]() cos
cos ![]() ),函数f(x)=
),函数f(x)= ![]()
(1)求函数f(x)的最小正周期;
(2)若f(α﹣ ![]() )=
)= ![]() ,求f(2α+
,求f(2α+ ![]() )的值.
)的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]()
![]() 经过点
经过点 ![]() ,其离心率
,其离心率 ![]() .
.
(Ⅰ)求椭圆 ![]() 的方程;
的方程;
(Ⅱ)设动直线 ![]() 与椭圆
与椭圆 ![]() 相切,切点为
相切,切点为 ![]() ,且
,且 ![]() 与直线
与直线 ![]() 相交于点
相交于点 ![]() .
.
试问:在 ![]() 轴上是否存在一定点,使得以
轴上是否存在一定点,使得以 ![]() 为直径的圆恒过该定点?若存在,
为直径的圆恒过该定点?若存在,
求出该点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2﹣alnx+x(a∈R)
(Ⅰ)当a=1时,求曲线y=f(x)在点A(1,f(1))处的切线方程;
(Ⅱ)讨论函数y=f(x)的单调性.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com