
【题目】已知函数f(x)=eax(a≠0).
(1)当 ![]() 时,令
时,令 ![]() (x>0),求函数g(x)在[m,m+1](m>0)上的最小值;
(x>0),求函数g(x)在[m,m+1](m>0)上的最小值;
(2)若对于一切x∈R,f(x)﹣x﹣1≥0恒成立,求a的取值集合;
(3)求证: ![]() .
.
【答案】
(1)解:当a= ![]() 时,g(x)=
时,g(x)= ![]() ,则g'(x)=
,则g'(x)= ![]() .
.
当 ![]() ﹣1>0,即x>2时,g'(x)>0;
﹣1>0,即x>2时,g'(x)>0;
当 ![]() ﹣1<0且x≠0,即x<2或0<x<2时,g'(x)<0.
﹣1<0且x≠0,即x<2或0<x<2时,g'(x)<0.
则g(x)的增区间为(2,+∞),减区间为(﹣∞,0),(0,2).
因为m>0,所以m+1>1,
①当m+1≤2,即0<m≤1时,g(x)在[m,m+1]上单调递减,
所以g(x)min=g(m+1)= ![]()
②当m<2<m+1,即1<m<2时,g(x)在[m,2]上单调递减,
在[2,m+1]上单调递增,所以g(x)min=g(2)= ![]()
③当m≥2时,g(x)在[m,m+1]上单调递增,所以g(x)min=g(m)= ![]() .
.
综上,g(x)min= 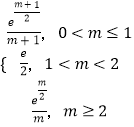
(2)解:设h(x)=f(x)﹣x﹣1=eax﹣x﹣1
若a<0,则对一切x>0,h(x)<0这与题设矛盾.
又a≠0,故a>0.而h'(x)=aeax﹣1,令h'(x)=0,得x= ![]() ,
,
当x< ![]() 时,h'(x)<0,h(x)单调递减;
时,h'(x)<0,h(x)单调递减;
当x> ![]() 时,h'(x)>0,h(x)单调递增.
时,h'(x)>0,h(x)单调递增.
故当x= ![]() 时,h(x)取最小值
时,h(x)取最小值 ![]() ﹣
﹣ ![]() ﹣1.
﹣1.
于是对一切x∈R,h(x)≥0恒成立,当且仅当 ![]() ﹣1≥0①
﹣1≥0①
令φ(x)=t﹣tlnt﹣1,则φ'(x)=﹣lnt
当0<t<1时,φ'(t)>0,φ(t)单调递增;
当t>1时,φ'(t)<0,φ(t)单调递减,
故当t=1时,φ(t)取最大值φ(1)=0,
因此,当且仅当 ![]() =1,即a=1时,①式成立.
=1,即a=1时,①式成立.
综上所述,a的取值集合为{1}
(3)证明:由(2)可知,当x>0时,g(x)= ![]() ,
,
所以 ![]() (x>0),
(x>0),
可得 ![]() ≤
≤ ![]()
于是 ![]() +
+ ![]()
≤ ![]()
< ![]()
= ![]() <
< ![]()
【解析】(1)求出函数的导数,解关于导函数的表达式,求出函数的单调区间,通过讨论m的范围求出函数的最小值即可;(2)设h(x)=f(x)﹣x﹣1=eax﹣x﹣1,求出a>0,解根据导函数的不等式,求出函数的单调区间,得到当且仅当 ![]() ﹣1≥0①令φ(x)=t﹣tlnt﹣1,根据函数的单调性求出a的范围即可;(3)由g(x)=
﹣1≥0①令φ(x)=t﹣tlnt﹣1,根据函数的单调性求出a的范围即可;(3)由g(x)= ![]() ,可得
,可得 ![]() ≤
≤ ![]() ,根据不等式的性质证明即可.
,根据不等式的性质证明即可.


科目:高中数学 来源: 题型:
【题目】由于研究性学习的需要,中学生李华持续收集了手机“微信运动”团队中特定20名成员每天行走的步数,其中某一天的数据记录如下: 5860 6520 7326 6798 7325
8430 8215 7453 7446 6754
7638 6834 6460 6830 9860
8753 9450 9860 7290 7850
对这20个数据按组距1000进行分组,并统计整理,绘制了如下尚不完整的统计图表:
步数分组统计表(设步数为x)
组别 | 步数分组 | 频数 |
A | 5500≤x<6500 | 2 |
B | 6500≤x<7500 | 10 |
C | 7500≤x<8500 | m |
D | 8500≤x<9500 | 2 |
E | 9500≤x<10500 | n |
(Ⅰ)写出m,n的值,并回答这20名“微信运动”团队成员一天行走步数的中位数落在哪个组别;
(Ⅱ)记C组步数数据的平均数与方差分别为v1 , ![]() ,E组步数数据的平均数与方差分别为v2 ,
,E组步数数据的平均数与方差分别为v2 , ![]() ,试分别比较v1与v2 ,
,试分别比较v1与v2 , ![]() 与
与 ![]() 的大小;(只需写出结论)
的大小;(只需写出结论)
(Ⅲ)从上述A,E两个组别的数据中任取2个数据,记这2个数据步数差的绝对值为ξ,求ξ的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知平面向量 ![]() ,
, ![]() ,
, ![]() 满足|
满足| ![]() |=|
|=| ![]() |=
|= ![]() ,|
,| ![]() |=1,若(
|=1,若( ![]() ﹣
﹣ ![]() )(
)( ![]() ﹣
﹣ ![]() )=0,则|
)=0,则| ![]() ﹣
﹣ ![]() |的取值范围是( )
|的取值范围是( )
A.[1,2]
B.[2,4]
C.[ ![]() ﹣1,
﹣1, ![]() +1]
+1]
D.[ ![]() ﹣1,
﹣1, ![]() +1]
+1]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,为测量山高MN,选择A和另一座山的山顶C为测量观测点.从A点测得 M点的仰角∠MAN=60°,C点的仰角∠CAB=45°以及∠MAC=75°;从C点测得∠MCA=60°.已知山高BC=100m,则山高MN=m. 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2cos22x﹣2,给出下列命题: ①β∈R,f(x+β)为奇函数;
②α∈(0, ![]() ),f(x)=f(x+2α)对x∈R恒成立;
),f(x)=f(x+2α)对x∈R恒成立;
③x1 , x2∈R,若|f(x1)﹣f(x2)|=2,则|x1﹣x2|的最小值为 ![]() ;
;
④x1 , x2∈R,若f(x1)=f(x2)=0,则x1﹣x2=kπ(k∈Z).其中的真命题有( )
A.①②
B.③④
C.②③
D.①④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C:(x+1)2+y2=8,点A(1,0),P是圆C上任意一点,线段AP的垂直平分线交CP于点Q,当点P在圆上运动时,点Q的轨迹为曲线E.
(1)求曲线E的方程;
(2)若直线l:y=kx+m与曲线E相交于M,N两点,O为坐标原点,求△MON面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l:x+ay﹣1=0是圆C:x2+y2﹣4x﹣2y+1=0的一条对称轴,过点A(﹣4,a)作圆C的两条切线,切点分别为B、D,则直线BD的方程为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xoy中,以O为极点,x轴的正半轴为极轴的极坐标系中,直线l的极坐标方程为θ= ![]() ,曲线C的参数方程为
,曲线C的参数方程为 ![]() .
.
(1)写出直线l与曲线C的直角坐标方程;
(2)过点M平行于直线l1的直线与曲线C交于A、B两点,若|MA||MB|= ![]() ,求点M轨迹的直角坐标方程.
,求点M轨迹的直角坐标方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com