
【题目】某种树苗栽种时高度为A(A为常数)米,栽种n年后的高度记为f(n).经研究发现f(n)近似地满足 f(n)=![]() ,其中
,其中![]() ,a,b为常数,n∈N,f(0)=A.已知栽种3年后该树木的高度为栽种时高度的3倍.
,a,b为常数,n∈N,f(0)=A.已知栽种3年后该树木的高度为栽种时高度的3倍.
(1)栽种多少年后,该树木的高度是栽种时高度的8倍;
(2)该树木在栽种后哪一年的增长高度最大.
【答案】(1)栽种![]() 年后,该树木的高度是栽种时高度的
年后,该树木的高度是栽种时高度的![]() 倍;(2)第
倍;(2)第![]() 年的增长高度最大.
年的增长高度最大.
【解析】
试题(1)由题中所给条件![]() ,运用待定系数法不难求出
,运用待定系数法不难求出![]() ,进而确定出函数
,进而确定出函数![]() ,其中
,其中![]() .由
.由![]() ,运用解方程的方法即可求出
,运用解方程的方法即可求出![]() ,问题得解; (2)由前面(1)中已求得
,问题得解; (2)由前面(1)中已求得![]() ,可表示出第n年的增长高度为
,可表示出第n年的增长高度为![]()
![]() ,这是一个含有较多字母的式子,这也中本题的一个难点,运用代数化简和整体思想可得:
,这是一个含有较多字母的式子,这也中本题的一个难点,运用代数化简和整体思想可得:![]() ,观察此式特征能用基本不等式的方法进行求它的最值,即:
,观察此式特征能用基本不等式的方法进行求它的最值,即: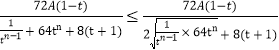 ,成立的条件为 当且仅当
,成立的条件为 当且仅当![]() 时取等号,即可求出
时取等号,即可求出![]() .
.
试题解析: (1)由题意知![]() .
.
所以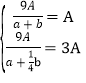 解得
解得![]() . 4分
. 4分
所以![]() ,其中
,其中![]() .
.
令![]() ,得
,得![]() ,解得
,解得![]() ,
,
所以![]() .
.
所以栽种9年后,该树木的高度是栽种时高度的8倍. 6span>分
(2)由(1)知![]() .
.
第n年的增长高度为![]()
![]() . 9分
. 9分
所以![]()
![]() 12分
12分
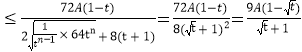 .
.
当且仅当![]() ,即
,即![]() 时取等号,此时
时取等号,此时![]() .
.
所以该树木栽种后第5年的增长高度最大. 14分


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】若关于x的方程(x﹣1)4+mx﹣m﹣2=0各个实根x1 , x2…xk(k≤4,k∈N*)所对应的点(xi![]() ),(i=1,2,3…k)均在直线y=x的同侧,则实数m的取值范围是( )
),(i=1,2,3…k)均在直线y=x的同侧,则实数m的取值范围是( )
A.(﹣1,7)
B.(﹣∞,﹣7)U(﹣1,+∞)
C.(﹣7,1)
D.(﹣∞,1)U(7,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,△ABC是边长为4的等边三角形,△ABD是等腰直角三角形,AD⊥BD,平面ABC⊥平面ABD,且EC⊥平面ABC,EC=2.
(1)证明:DE∥平面ABC;
(2)证明:AD⊥BE.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知极坐标系的极点在直角坐标系的原点处,极轴与x轴的正半轴重合.直线l的参数方程为: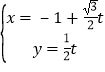 (t为参数),曲线C的极坐标方程为:ρ=4cosθ.
(t为参数),曲线C的极坐标方程为:ρ=4cosθ.
(Ⅰ)写出C的直角坐标方程,并指出C是什么曲线;
(Ⅱ)设直线l与曲线C相交于P、Q两点,求|PQ|值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}(n=1,2,3,4,5)满足a1=a5=0,且当2≤k≤5时,(ak﹣ak﹣1)2=1,令S=![]() , 则S不可能的值是( )
, 则S不可能的值是( )
A.4
B.0
C.1
D.-4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在区间[a,b]上的连续函数y=f(x),如果![]() ,使得
,使得![]() ,则称
,则称![]() 为区间[a,b]上的“中值点”,下列函数:
为区间[a,b]上的“中值点”,下列函数:
①![]() ; ②
; ②![]() ; ③
; ③![]() ; ④
; ④![]() 中,在区间[O,1]上“中值点”多于一个的函数序号为( )
中,在区间[O,1]上“中值点”多于一个的函数序号为( )
A. ①② B. ①③ C. ②③ D. ①④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com