
【题目】已知函数![]() 是
是![]() 上的偶函数.
上的偶函数.
(1)求实数![]() 的值;
的值;
(2)判断并证明函数![]() 在
在![]() 上单调性;
上单调性;
(3)求函数![]() 在
在![]() 上的最大值与最小值.
上的最大值与最小值.
科目:高中数学 来源: 题型:
【题目】现有 ![]() 个人去参加某娱乐活动,该活动有甲、乙两个游戏可供参加者选择.为增加趣味性,
个人去参加某娱乐活动,该活动有甲、乙两个游戏可供参加者选择.为增加趣味性,
约定:每个人通过掷一枚质地均匀的骰子决定自己去参加哪个游戏,掷出点数为 ![]() 或
或 ![]() 的人去参加
的人去参加
甲游戏,掷出点数大于 ![]() 的人去参加乙游戏.
的人去参加乙游戏.
(1)求这 ![]() 个人中恰有
个人中恰有 ![]() 个人去参加甲游戏的概率;
个人去参加甲游戏的概率;
(2)求这 ![]() 个人中去参加甲游戏的人数大于去参加乙游戏的人数的概率.
个人中去参加甲游戏的人数大于去参加乙游戏的人数的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)当![]() 时,证明函数
时,证明函数![]() 在
在![]() 是单调函数;
是单调函数;
(2)当![]() 时,函数
时,函数![]() 在区间
在区间![]() 上的最小值是
上的最小值是![]() ,求
,求![]() 的值;
的值;
(3)设![]() ,
,![]() 是函数
是函数![]() 图象上任意不同的两点,记线段
图象上任意不同的两点,记线段![]() 的中点的横坐标是
的中点的横坐标是![]() ,证明直线
,证明直线![]() 的斜率
的斜率![]()
![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正三棱柱ABCA1B1C1中,F,F1分别是AC,A1C1的中点.
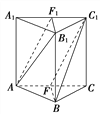
求证:(1)平面AB1F1∥平面C1BF;
(2)平面AB1F1⊥平面ACC1A1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某投资人欲将5百万元奖金投入甲、乙两种理财产品,根据银行预测,甲、乙两种理财产品的收益与投入奖金![]() 的关系式分别为
的关系式分别为![]() ,其中
,其中![]() 为常数且
为常数且![]() .设对乙种产品投入奖金
.设对乙种产品投入奖金![]() 百万元,其中
百万元,其中![]() .
.
(1)当![]() 时,如何进行投资才能使得总收益
时,如何进行投资才能使得总收益![]() 最大;(总收益
最大;(总收益![]() )
)
(2)银行为了吸储,考虑到投资人的收益,无论投资人奖金如何分配,要使得总收益不低于![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某少数民族的刺绣有着悠久的历史,下图![]() 为她们刺绣最简单的四个图案,这些图案都由小正方形构成,小正方形数越多刺绣越漂亮,现按同样的规律刺绣(小正方形的摆放规律相同),设第n个图形包含
为她们刺绣最简单的四个图案,这些图案都由小正方形构成,小正方形数越多刺绣越漂亮,现按同样的规律刺绣(小正方形的摆放规律相同),设第n个图形包含![]() 个小正方形.
个小正方形.

(1)求出![]() ;
;
(2)利用合情推理的“归纳推理思想”归纳出![]() 与
与![]() 的关系式,
的关系式,
(3)根据你得到的关系式求![]() 的表达式
的表达式
查看答案和解析>>
科目:高中数学 来源: 题型:
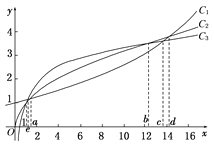
【题目】函数f(x)=1.1x,g(x)=ln x+1,h(x)=x![]() 的图象如图所示,试分别指出各曲线对应的函数,并比较三个函数的增长差异(以1,a,b,c,d,e为分界点).
的图象如图所示,试分别指出各曲线对应的函数,并比较三个函数的增长差异(以1,a,b,c,d,e为分界点).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】网上购物系统是一种具有交互功能的商业信息系统,它在网络上建立一个虚拟的购物商场,使购物过程变得轻松、快捷、方便.网上购物系统分为前台管理和后台管理,前台管理包括浏览商品、查询商品、订购商品、用户注册等功能;后台管理包括公告管理、商品管理、订单管理、投诉管理和用户管理等模块.根据这些要求画出该系统的结构图.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com