Question

9£®ÒÑ֪ƽÃæÖ±½Ç×ø±êϵxoyÄÚÁ½¸ö¶¨µãA£¨1£¬0£©¡¢B£¨4£¬0£©£¬Âú×ãPB=2PAµÄµãP£¨x£¬y£©ÐγɵÄÇúÏß¼ÇΪ¦££®
£¨1£©ÇóÇúÏߦ£µÄ·½³Ì£»
£¨2£©¹ýµãBµÄÖ±ÏßlÓëÇúÏߦ£ÏཻÓÚC¡¢DÁ½µã£¬µ±¡÷CODµÄÃæ»ý×î´óʱ£¬ÇóÖ±ÏßlµÄ·½³Ì£¨OΪ×ø±êÔ­µã£©£»
£¨3£©ÉèÇúÏߦ£·Ö±ð½»x¡¢yÖáµÄÕý°ëÖáÓÚM¡¢NÁ½µã£¬µãQÊÇÇúÏߦ£Î»ÓÚµÚÈýÏóÏÞÄÚÒ»¶ÎÉϵÄÈÎÒâÒ»µã£¬Á¬½áQN½»xÖáÓÚµãE¡¢Á¬½áQM½»yÖáÓÚF£®ÇóÖ¤ËıßÐÎMNEFµÄÃæ»ýΪ¶¨Öµ£®

Answer 1

·ÖÎö £¨1£©ÓÉÁ½¸ö¶¨µãA£¨1£¬0£©¡¢B£¨4£¬0£©£¬Âú×ãPB=2PAµÄµãP£¨x£¬y£©£¬µÃµ½¹Øϵʽ»¯¼ò¼´¿ÉµÃ³öÇúÏߦ£µÄ·½³Ì£»
£¨2£©±íʾ³öÃæ»ý£¬ÀûÓûù±¾²»µÈʽµÃ³ö½áÂÛ£»
£¨3£©Éè${S_{MNEF}}={S_{¡÷MNE}}+{S_{¡÷MEF}}=\frac{1}{2}ME•NF$£¬¼´¿ÉÖ¤Ã÷½áÂÛ£®

½â´ð ½â£º£¨1£©ÓÉÌâÉèÖª$2\sqrt{{{£¨x-1£©}^2}+{y^2}}=\sqrt{{{£¨x-4£©}^2}+{y^2}}$£¬Á½±ß»¯¼òµÃx²+y²=4
¡àµãPµÄ¹ì¼£¦£µÄ·½³ÌΪx²+y²=4¡­£¨3·Ö£©
£¨2£©ÓÉÌâÒâÖª$OS=\sqrt{S{D^2}-O{D^2}}=\sqrt{3}$µÄбÂÊÒ»¶¨´æÔÚ£¬Éèl£ºy=k£¨x-4£©¼´kx-y-4k=0£¬
¡ßÔ­µãµ½Ö±ÏßlµÄ¾àÀë$d=\frac{{|{4k}|}}{{\sqrt{1+{k^2}}}}£¬CD=2\sqrt{4-{d^2}}$£¬¡­£¨5·Ö£©
¡à${S_{¡÷COD}}=\frac{1}{2}CD•d=\sqrt{{d^2}•£¨4-{d^2}£©}¡Ü\sqrt{{{£¨\frac{{{d^2}+£¨4-{d^2}£©}}{2}£©}^2}}=2$£¬¡­£¨7·Ö£©
µ±ÇÒ½öµ±d²=2ʱ£¬È¡µÃ¡°=¡±d²=2£¼r²=4
¡àµ±d²=2ʱ£¬´Ëʱ£¬$\frac{{16{k^2}}}{{{k^2}+1}}=2⇒{k^2}=\frac{1}{7}⇒k=¡À\frac{{\sqrt{7}}}{7}$£®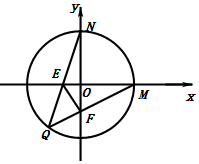

¡àÖ±ÏßlµÄ·½³ÌΪ$y=¡À\frac{{\sqrt{7}}}{7}£¨x-4£©$£®¡­£¨9·Ö£©
£¨3£©Éè${S_{MNEF}}={S_{¡÷MNE}}+{S_{¡÷MEF}}=\frac{1}{2}ME•NF$¡­£¨11·Ö£©
ÉèQ£¨x₀£¬y₀£©£¬E£¨e£¬0£©£¬F£¨0£¬f£©£¨ÆäÖÐ${x_0}£¼0£¬{y_0}£¼0£¬{x_0}^2+{y_0}^2=4$£©
Ôò$QM£ºy=\frac{y_0}{{{x_0}-2}}£¨x-2£©$£¬Áîx=0µÃ$f=\frac{{-2{y_0}}}{{{x_0}-2}}$
¡à$NF=2-\frac{{-2{y_0}}}{{{x_0}-2}}=\frac{{2£¨{x_0}+{y_0}£©-4}}{{{x_0}-2}}$¡­£¨12·Ö£©$QN£ºy=\frac{{{y_0}-2}}{x_0}x+2$£¬Áîy=0µÃ$e=\frac{{2{x_0}}}{{2-{y_0}}}$
¡à$ME=2-\frac{{2{x_0}}}{{2-{y_0}}}=\frac{{4-2£¨{x_0}+{y_0}£©}}{{2-{y_0}}}$¡­£¨13·Ö£©
¡à${S_{MNEF}}=\frac{1}{2}ME•NF=\frac{1}{2}•\frac{{2£¨{x_0}+{y_0}£©-4}}{{{x_0}-2}}•\frac{{2£¨{x_0}+{y_0}£©-4}}{{{y_0}-2}}=2•\frac{{{{£¨{x_0}+{y_0}-2£©}^2}}}{{£¨{x_0}-2£©£¨{y_0}-2£©}}$=$2•\frac{{{{£¨{x_0}+{y_0}-2£©}^2}}}{{£¨{x_0}-2£©£¨{y_0}-2£©}}=2•\frac{{8-4£¨{x_0}+{y_0}£©+2{x_0}{y_0}}}{{4-2£¨{x_0}+{y_0}£©+{x_0}{y_0}}}=4$£¨¶¨Öµ£©¡­£¨16·Ö£©

µãÆÀ ±¾Ì⿼²é¹ì¼£·½³Ì£¬¿¼²éÃæ»ýµÄ¼ÆË㣬¿¼²é»ù±¾²»µÈʽµÄÔËÓã¬ÊôÓÚÖеµÌ⣮