
【题目】如图,在多面体![]() 中,四边形
中,四边形![]() 和
和![]() 都是直角梯形,
都是直角梯形,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,,
,,![]() 是
是![]() 的中点。
的中点。
(1)求证:![]() ;
;
(2)已知![]() 是
是![]() 的中点,求证:
的中点,求证:![]() ;
;
(3)求直线![]() 与平面
与平面![]() 所成角的大小。
所成角的大小。
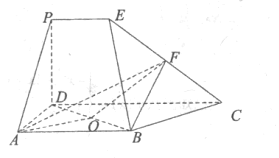
【答案】(1)见解析;(2)见解析;(3)![]() .
.
【解析】
(1)取PD中点G,连结GF,AG,推导出四边形ABFG是平行四边形,从而AG∥BF,进而能证明BF∥平面ADP.
(2)已知O是BD的中点,证明FO⊥BD,AO⊥BD,即可证明:BD⊥平面AOF.
(2)以D为原点,DA为x轴,DC为y轴,DP为z轴,建立空间直角坐标系,由(2)可知![]() 为平面
为平面![]() 的法向量,利用向量法直线
的法向量,利用向量法直线![]() 与平面
与平面![]() 所成角的大小.
所成角的大小.
(1)取PD中点G,连结GF,AG,
∵AB∥DC,PE∥DC,AD⊥DC,PD⊥平面ABCD,AB=PD=DA=2PE,CD=3PE,F是CE的中点,
∴FG![]() AB,∴四边形ABFG是平行四边形,∴AG∥BF,
AB,∴四边形ABFG是平行四边形,∴AG∥BF,
∵AG平面ADP,BF平面ADP,∴BF∥平面ADP.
(2)由(1)可知FM=PE,DM=BM=2PE,∴FD=FB![]() PE,
PE,
∵O是BD的中点,∴FO⊥BD,
∵AD=AB,O是BD的中点,∴AO⊥BD,
∵AO∩FO=O,
∴BD⊥平面AOF.
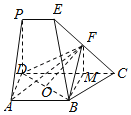
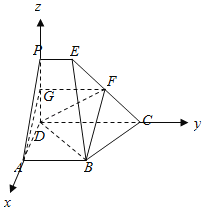
(3)以D为原点,DA为x轴,DC为y轴,DP为z轴,建立空间直角坐标系,
设PE=1,则B(2,2,0),D(0,0,0),P(0,0,2),C(0,3,0),E(0,1,2),F(0,2,1),
![]() (2,2,0),
(2,2,0),![]() (0,-1,1),
(0,-1,1),
由(2)可知![]() 为平面
为平面![]() 的法向量,
的法向量,
设直线![]() 与平面
与平面所成角为θ,
则sinθ=cos<![]() >
>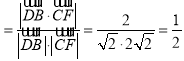 .
.
∴θ=![]() .
.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:高中数学 来源: 题型:
【题目】如图,直角梯形ABCD中,AB∥CD,∠BAD=90°,AB=AD=1,CD=2,若将△BCD沿着BD折起至△BC'D,使得AD⊥BC'.

(1)求证:平面C'BD⊥平面ABD;
(2)求C'D与平面ABC'所成角的正弦值;
(3)M为BD中点,求二面角M﹣AC'﹣B的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线E的极坐标方程为4(ρ2-4)sin2θ=(16-ρ2)cos2θ,以极轴为x轴的非负半轴,极点O为坐标原点,建立平面直角坐标系.
(1)写出曲线E的直角坐标方程;
(2)若点P为曲线E上动点,点M为线段OP的中点,直线l的参数方程为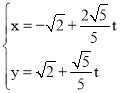 (t为参数),求点M到直线l的距离的最大值.
(t为参数),求点M到直线l的距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() 分别为双曲线
分别为双曲线![]()
![]()
![]() 的左、右焦点,点P是以
的左、右焦点,点P是以![]() 为直径的圆与C在第一象限内的交点,若线段
为直径的圆与C在第一象限内的交点,若线段![]() 的中点Q在C的渐近线上,则C的两条渐近线方程为__________.
的中点Q在C的渐近线上,则C的两条渐近线方程为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an+1﹣an}是首项为![]() ,公比为
,公比为![]() 的等比数列,a1=1.
的等比数列,a1=1.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)求数列{(3n﹣1)an}的前n项和Sn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某蔬果经销商销售某种蔬果,售价为每公斤25元,成本为每公斤15元.销售宗旨是当天进货当天销售.如果当天卖不出去,未售出的全部降价以每公斤10元处理完.根据以往的销售情况,得到如图所示的频率分布直方图:

(1)根据频率分布直方图计算该种蔬果日需求量的平均数![]() (同一组中的数据用该组区间中点值代表);
(同一组中的数据用该组区间中点值代表);
(2)该经销商某天购进了250公斤这种蔬果,假设当天的需求量为![]() 公斤
公斤![]() ,利润为
,利润为![]() 元.求
元.求![]() 关于
关于![]() 的函数关系式,并结合频率分布直方图估计利润
的函数关系式,并结合频率分布直方图估计利润![]() 不小于1750元的概率.
不小于1750元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场从2018年1月份起的前这个月,顾客对某商品的需求总量,![]() (单位:件)与x的关系近似地满足
(单位:件)与x的关系近似地满足![]() (其中
(其中![]() ,且
,且![]() ),该商品第x月的进货单价
),该商品第x月的进货单价![]() (单位:元)与x的近似关系是
(单位:元)与x的近似关系是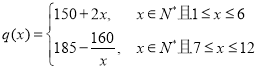 .
.
(1)写出2018年第x月的需求量![]() (单位:件)与x的函数关系式;
(单位:件)与x的函数关系式;
(2)该商品每件的售价为185元,若不计其他费用且每月都能满足市场需求,试问该商场2018年第几个月销售该商品的月利润![]() 最大,最大月利润为多少元?
最大,最大月利润为多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直角三角形![]() 所在的平面与半圆弧
所在的平面与半圆弧![]() 所在平面相交于
所在平面相交于![]() ,
,![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,
的中点, ![]() 是
是![]() 上异于
上异于![]() ,
,![]() 的点,
的点, ![]() .
.
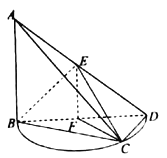
(1)证明:平面![]() 平面
平面![]() ;
;
(2)若点![]() 为半圆弧
为半圆弧![]() 上的一个三等分点(靠近点
上的一个三等分点(靠近点![]() )求二面角
)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com