
【题目】已知椭圆![]() :
:![]() ,
,![]() 为坐标原点,
为坐标原点,![]() 为椭圆
为椭圆![]() 的左焦点,离心率为
的左焦点,离心率为![]() ,直线
,直线![]() 与椭圆相交于
与椭圆相交于![]() ,
,![]() 两点.
两点.
(1)求椭圆![]() 的方程;
的方程;
(2)若![]() 是弦
是弦![]() 的中点,
的中点,![]() 是椭圆
是椭圆![]() 上一点,求
上一点,求![]() 的面积最大值.
的面积最大值.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)根据![]() 可求得
可求得![]() ,结合离心率为
,结合离心率为![]() 即可求得
即可求得![]() ,
,![]() ,问题得解。
,问题得解。
(2)设![]() ,
,![]() .设直线
.设直线![]() 的方程为:
的方程为:![]() ,联立直线与椭圆方程可得:
,联立直线与椭圆方程可得:![]() ,结合
,结合![]() 可求得
可求得![]() ,利用弦长公式求得
,利用弦长公式求得![]() ,再利用直线与椭圆的位置关系即可求出
,再利用直线与椭圆的位置关系即可求出![]() 点到直线
点到直线![]() 的距离的最大值,问题得解。
的距离的最大值,问题得解。
解:∵![]() ,
,![]() 为椭圆
为椭圆![]() 的左焦点,
的左焦点,
设椭圆![]() 的焦距为
的焦距为![]() ,所以
,所以![]() ,
,
∵离心率为![]() ,∴
,∴![]() ,又
,又![]() ,所以
,所以![]() ,
,
∴椭圆![]() 的方程为:
的方程为:![]() .
.
(2)设![]() ,
,![]() .
.
∵![]() 是弦
是弦![]() 的中点,∴直线
的中点,∴直线![]() 的斜率存在,设斜率为
的斜率存在,设斜率为![]() ,
,
则直线![]() 的方程为:
的方程为:![]() ,即
,即![]() .
.
由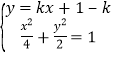 联立,整理得:
联立,整理得:![]() ,
,
因为直线与椭圆相交,所以![]() 成立.
成立.
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴直线![]() 的方程为:
的方程为:![]() ,
,![]() ,
,![]() ,
,
∴![]()
![]() .
.
要使![]() 的面积最大值,而
的面积最大值,而![]() 是定值,需
是定值,需![]() 点到
点到![]() 的距离最大即可.
的距离最大即可.
设与直线![]() 平行的直线方程为:
平行的直线方程为:![]() ,
,
由方程组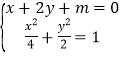 联立,得
联立,得![]() ,
,
令![]() ,得
,得![]() .
.
∵![]() 是椭圆
是椭圆![]() 上一点,
上一点,
∴![]() 点到
点到![]() 的最大距离,即直线
的最大距离,即直线![]() 到直线
到直线![]() 的距离
的距离![]() .
.
而![]() ,
,
此时![]()
![]() .
.
因此,![]() 的面积最大值为
的面积最大值为![]() .
.


 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案科目:高中数学 来源: 题型:
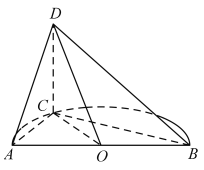
【题目】如图,已知点C是圆心为O半径为1的半圆弧上从点A数起的第一个三等分点,![]() 是直径,
是直径,![]() ,直线
,直线![]() 平面
平面![]() .
.
(1)证明:![]() ;
;
(2)若M为![]() 的中点,求证:
的中点,求证:![]() 平面
平面![]() ;
;
(3)求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在①![]() ;②
;②![]() 这两个条件中任选-一个,补充在下面问题中,然后解答补充完整的题.
这两个条件中任选-一个,补充在下面问题中,然后解答补充完整的题.

在![]() 中,角
中,角![]() 的对边分别为
的对边分别为![]() ,已知 ,
,已知 ,![]() .
.
(1)求![]() ;
;
(2)如图,![]() 为边
为边![]() 上一点,
上一点,![]() ,求
,求![]() 的面积
的面积
查看答案和解析>>
科目:高中数学 来源: 题型:
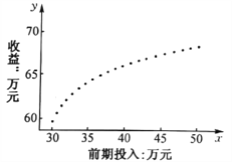
【题目】某互联网公司为了确定下一季度的前期广告投入计划,收集了近期前期广告投入量![]() (单位:万元)和收益
(单位:万元)和收益![]() (单位:万元)的数据。对这些数据作了初步处理,得到了下面的散点图(共
(单位:万元)的数据。对这些数据作了初步处理,得到了下面的散点图(共![]() 个数据点)及一些统计量的值.为了进一步了解广告投入量
个数据点)及一些统计量的值.为了进一步了解广告投入量![]() 对收益
对收益![]() 的影响,公司三位员工①②③对历史数据进行分析,查阅大量资料,分别提出了三个回归方程模型:
的影响,公司三位员工①②③对历史数据进行分析,查阅大量资料,分别提出了三个回归方程模型:
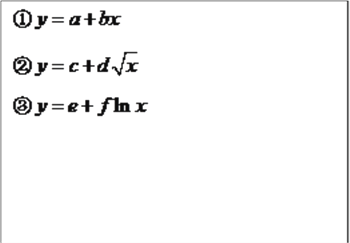
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
根据![]() ,
, ![]() ,参考数据:
,参考数据: ![]() ,
, ![]() .
.
(1)根据散点图判断,哪一位员工提出的模型不适合用来描述![]() 与
与![]() 之间的关系?简要说明理由.
之间的关系?简要说明理由.
(2)根据(1)的判断结果及表中数据,在余下两个模型中分别建立收益![]() 关于投入量
关于投入量![]() 的关系,并从数据相关性的角度考虑,在余下两位员工提出的回归模型中,哪一个是最优模型(即更适宜作为收益
的关系,并从数据相关性的角度考虑,在余下两位员工提出的回归模型中,哪一个是最优模型(即更适宜作为收益![]() 的回归方程)?说明理由;
的回归方程)?说明理由;
附:对于一组数据![]() ,
, ![]() ,…,
,…, ![]() ,其回归直线
,其回归直线![]() 的斜率、截距的最小二乘估计以及相关系数分别为:
的斜率、截距的最小二乘估计以及相关系数分别为:
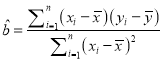 ,
, ![]() ,
, 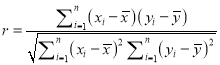 ,
,
其中![]() 越接近于
越接近于![]() ,说明变量
,说明变量![]() 与
与![]() 的线性相关程度越好.
的线性相关程度越好.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() 的离心率为
的离心率为![]() ,长半轴长为短轴长的b倍,A,B分别为椭圆C的上、下顶点,点
,长半轴长为短轴长的b倍,A,B分别为椭圆C的上、下顶点,点![]() .
.
![]() 求椭圆C的方程;
求椭圆C的方程;
![]() 若直线MA,MB与椭圆C的另一交点分别为P,Q,证明:直线PQ过定点.
若直线MA,MB与椭圆C的另一交点分别为P,Q,证明:直线PQ过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在空格内填入“充分非必要”或“必要非充分”或“充要”或“既非充分又非必要”.
(1)“![]() ”是“
”是“![]() ”的________条件;
”的________条件;
(2)“![]() ”是“
”是“![]() ”的________条件;
”的________条件;
(3)已知![]() ,
,![]() ,“
,“![]() ”是“
”是“![]() ”的________条件;
”的________条件;
(4)“![]() ”是“
”是“![]() ”的________条件;
”的________条件;
(5)“![]() ”是“AB”的________条件;
”是“AB”的________条件;
(6)“![]() ”是“
”是“![]() ”的________条件;
”的________条件;
(7)“集合AB”是“![]() ”的________条件;
”的________条件;
(8)已知![]() ,“
,“![]() ”是“
”是“![]() ”的________条件.
”的________条件.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com