
【题目】阿波罗尼斯(古希腊数学家,约公元前262-190年)的著作《圆锥曲线论》是古代世界光辉的科学成果,它将圆锥曲线的性质网罗殆尽,几乎使后人没有插足的余地.他证明过这样一个命题:平面内与两定点距离的比为常数![]() 的点的轨迹是圆,后人将这个圆称为阿波罗尼斯圆.①若定点为
的点的轨迹是圆,后人将这个圆称为阿波罗尼斯圆.①若定点为![]() ,写出
,写出![]() 的一个阿波罗尼斯圆的标准方程__________;②△
的一个阿波罗尼斯圆的标准方程__________;②△![]() 中,
中,![]() ,则当△
,则当△![]() 面积的最大值为
面积的最大值为![]() 时,
时,![]() ______.
______.
科目:高中数学 来源: 题型:
【题目】为了比较两种治疗某病毒的药(分别称为甲药,乙药)的疗效,某医疗团队随机地选取了服用甲药的患者和服用乙药的患者进行研究,根据研究的数据,绘制了如图1等高条形图
.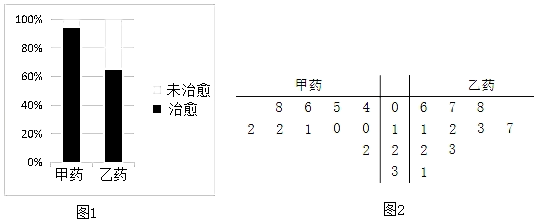
(1)根据等高条形图,判断哪一种药的治愈率更高,不用说明理由;
(2)为了进一步研究两种药的疗效,从服用甲药的治愈患者和服用乙药的治愈患者中,分别抽取了10名,记录他们的治疗时间(单位:天),统计并绘制了如图2茎叶图,从茎叶图看,哪一种药的疗效更好,并说明理由;
(3)标准差s除了可以用来刻画一组数据的离散程度外,还可以刻画每个数据偏离平均水平的程度,如果出现了治疗时间在(![]() 3s,
3s,![]() 3s)之外的患者,就认为病毒有可能发生了变异,需要对该患者进行进一步检查,若某服用甲药的患者已经治疗了26天还未痊愈,请结合(2)中甲药的数据,判断是否应该对该患者进行进一步检查?
3s)之外的患者,就认为病毒有可能发生了变异,需要对该患者进行进一步检查,若某服用甲药的患者已经治疗了26天还未痊愈,请结合(2)中甲药的数据,判断是否应该对该患者进行进一步检查?
参考公式:s![]() ,
,
参考数据:![]() 48.
48.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() ,
,![]() ,
,![]() .
.
(1)讨论函数![]() 的单调性;
的单调性;
(2)若![]() (其中
(其中![]() ),证明:
),证明:![]() ;
;
(3)是否存在实数a,使得![]() 在区间
在区间![]() 内恒成立,且关于x的方程
内恒成立,且关于x的方程![]() 在
在![]() 内有唯一解?请说明理由.
内有唯一解?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,以原点为极点,![]() 轴非负半轴为极轴,长度单位相同,建立极坐标系,曲线
轴非负半轴为极轴,长度单位相同,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 过点
过点![]() ,倾斜角为
,倾斜角为![]() .
.
(1)将曲线![]() 的极坐标方程化为直角坐标方程,写出直线
的极坐标方程化为直角坐标方程,写出直线![]() 的参数方程的标准形式;
的参数方程的标准形式;
(2)已知直线![]() 交曲线
交曲线![]() 于
于![]() 两点,求
两点,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
已知函数![]() 的反函数.定义:若对给定的实数
的反函数.定义:若对给定的实数![]() ,函数
,函数![]() 与
与![]() 互为反函数,则称
互为反函数,则称![]() 满足“
满足“![]() 和性质”;若函数
和性质”;若函数![]() 与
与![]() 互为反函数,则称
互为反函数,则称![]() 满足“
满足“![]() 积性质”.
积性质”.
(1) 判断函数![]() 是否满足“1和性质”,并说明理由;
是否满足“1和性质”,并说明理由;
(2) 求所有满足“2和性质”的一次函数;
(3) 设函数![]() 对任何
对任何![]() ,满足“
,满足“![]() 积性质”.求
积性质”.求![]() 的表达式.
的表达式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】四面体P﹣ABC中,PA![]() ,PB=PC=AB=AC=2,BC=2
,PB=PC=AB=AC=2,BC=2![]() ,动点Q在△ABC的内部(含边界),设∠PAQ=α,二面角P﹣BC﹣A的平面角的大小为β,△APQ和△BCQ的面积分别为S1和S2,且满足
,动点Q在△ABC的内部(含边界),设∠PAQ=α,二面角P﹣BC﹣A的平面角的大小为β,△APQ和△BCQ的面积分别为S1和S2,且满足![]() ,则S2的最大值为_____.
,则S2的最大值为_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为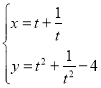 (
(![]() 为参数).
为参数).
(1)求曲线![]() 的普通方程;
的普通方程;
(2)以![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立极坐标系,直线
轴的非负半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() ,(
,(![]() ),直线
),直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点,求线段
两点,求线段![]() 的长度
的长度![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】家具公司制作木质的书桌和椅子,需要木工和漆工两道工序,已知木工平均四个小时做一把椅子,八个小时做一张书桌,该公司每星期木工最多有8000个工作时;漆工平均两小时漆一把椅子、一小时漆一张书桌,该公司每星期漆工最多有1300个工作时,又已知制作一把椅子和一张书桌的利润分别是15元和20元,试根据以上条件,问怎样安排生产能获得最大利润?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com