
【题目】已知 ![]() 的展开式各项系数和为M,
的展开式各项系数和为M, ![]() 的展开式各项系数和为N,(x+1)n的展开式各项的系数和为P,且M+N﹣P=2016,试求
的展开式各项系数和为N,(x+1)n的展开式各项的系数和为P,且M+N﹣P=2016,试求 ![]() 的展开式中:
的展开式中:
(1)二项式系数最大的项;
(2)系数的绝对值最大的项.
【答案】
(1)解:∵M+N﹣P=4n+2n+5﹣2n=(2n)2+312n=2016,
∴(2n)2+312n﹣2016=0,
∴(2n+63)(2n﹣32)=0,
∴2n=32,
∴n=5,
∴ ![]() 的展开式的通项
的展开式的通项 ![]() ,
,
![]() 的展开式共有11项,二项式系数最大的项为中间项第6项,其值为
的展开式共有11项,二项式系数最大的项为中间项第6项,其值为 ![]()
(2)解:第r+1项Tr+1的系数的绝对值为 ![]() ,
,
若第r+1项Tr+1的系数的绝对值最大,则{ 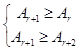 ,
,
可得 ![]() ,又r∈N*,∴r=3,
,又r∈N*,∴r=3,
故系数的绝对值最大的项为 ![]()
【解析】先求出n的值,再写出展开式的通项,(1)根据展开式的通项即可求出二项式系数最大的项,(2)若第r+1项Tr+1的系数的绝对值最大,得到关于r的不等式组,解得即可.


科目:高中数学 来源: 题型:
【题目】已知数列{an}满足a1=1,(an﹣3)an+1﹣an+4=0(n∈N*).
(1)求a2 , a3 , a4;
(2)猜想{an}的通项公式,并用数学归纳法证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某网站对“爱飞客”飞行大会的日关注量x(万人)与日点赞量y(万次)进行了统计对比,得到表格如下:
x | 3 | 5 | 6 | 7 | 9 |
y | 2 | 3 | 3 | 4 | 5 |
由散点图象知,可以用回归直线方程 ![]() 来近似刻画它们之间的关系.
来近似刻画它们之间的关系.
(Ⅰ)求出y关于x的回归直线方程,并预测日关注量为10万人时的日点赞量;
(Ⅱ)一个三口之家参加“爱飞客”亲子游戏,游戏规定:三人依次从装有3个白球和2个红球的箱子中不放回地各摸出一个球,大人摸出每个红球得奖金10元,小孩摸出1个红球得奖金50元.求该三口之家所得奖金总额不低于50元的概率.
参考公式:b= 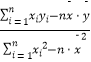 ; 参考数据:
; 参考数据: ![]() =200,
=200, ![]() =112.
=112.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等比数列{an}满足 ![]() ,n∈N* . (Ⅰ)求数列{an}的通项公式;
,n∈N* . (Ⅰ)求数列{an}的通项公式;
(Ⅱ)设数列{an}的前n项和为Sn , 若不等式Sn>kan﹣2对一切n∈N*恒成立,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(理科答)已知数列{an}及等差数列{bn},若a1=3,an= ![]() an﹣1+1(n≥2),a1=b2 , 2a3+a2=b4 ,
an﹣1+1(n≥2),a1=b2 , 2a3+a2=b4 ,
(1)证明数列{an﹣2}为等比数列;
(2)求数列{an}及数列{bn}的通项公式;
(3)设数列{anbn}的前n项和为Tn , 求Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知棱长为1的正方体ABCD﹣A1B1C1D1中,E,F分别是棱B1C1 , C1D1的中点. (Ⅰ)求AD1与EF所成角的大小;
(Ⅱ)求AF与平面BEB1所成角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线y2=2px(p>0)的焦点为(1,0),A,B是抛物线上位于x轴两侧的两动点,且 ![]() =﹣4(O为坐标原点).
=﹣4(O为坐标原点).
(1)求抛物线方程;
(2)证明:直线AB过定点T;
(3)过点T作AB的垂线交抛物线于M,N两点,求四边形AMBN的面积的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com